
 如图,在边长为L的等边三角形ACD区域内,存在垂直于所在平面向里的匀强磁场.大量的质量为m、电荷量为q的带正电粒子以相同速度(速度大小未确定)沿垂直于CD的方向射入磁场,经磁场偏转后三条边均有粒子射出,其中垂直于AD边射出的粒子在磁场中运动的时间为t0.不计粒子的重力及粒子间的相互作用.求:
如图,在边长为L的等边三角形ACD区域内,存在垂直于所在平面向里的匀强磁场.大量的质量为m、电荷量为q的带正电粒子以相同速度(速度大小未确定)沿垂直于CD的方向射入磁场,经磁场偏转后三条边均有粒子射出,其中垂直于AD边射出的粒子在磁场中运动的时间为t0.不计粒子的重力及粒子间的相互作用.求:分析 (1)根据几何关系求出粒子垂直AD射出时圆心角的大小,结合周期公式和运动的时间求出磁感应强度的大小.
(2)当轨迹圆与AC、AD都相切时,粒子能从CD边射出,半径最大,速度为最大值,根据几何关系求出半径,结合半径公式求出最大速度.
(3)当轨迹圆与AC相切时,从AC边射出的粒子距C最远,当轨迹圆与AD边的交点F恰在圆心O正上方时,射出的粒子距D点最远,结合几何 关系求出AC、AD边上可能有粒子射出的范围.
解答 解:(1)洛伦兹力提供向心力,有:$qvB=m\frac{v^2}{r}$
周期$T=\frac{2πr}{v}=\frac{2πm}{qB}$
当粒子垂直AD边射出时,根据几何关系有:圆心角为60°
${t_0}=\frac{1}{6}T$
联立解得$B=\frac{πm}{{3q{t_0}}}$.
(2)当轨迹圆与AC、AD都相切时,粒子能从CD边射出,半径最大,速度为最大值,此时
$r=\frac{L}{2}sin{60^o}=\frac{{\sqrt{3}}}{4}L$ 
根据$qvB=m\frac{v^2}{r}$得,
$r=\frac{mv}{qB}$,解得$v=\frac{{\sqrt{3}πL}}{{12{t_0}}}$
所以,粒子射入的速度应满足$v≤\frac{{\sqrt{3}πL}}{{12{t_0}}}$
(3)由(2)知,当轨迹圆与AC相切时,从AC边射出的粒子距C最远
故有粒子射出的范围为CE段,${x_{CE}}=\frac{L}{2}cos60°=\frac{L}{4}$
当轨迹圆与AD边的交点F恰在圆心O正上方时,射出的粒子距D点最远.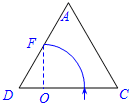
故有粒子射出的范围为DF段,${x_{DF}}=\frac{r}{{sin{{60}^o}}}=\frac{L}{2}$.
答:(1)磁场的磁感应强度大小为$\frac{πm}{3q{t}_{0}}$;
(2)要确保粒子能从CD边射出,射入的最大速度为$\frac{\sqrt{3}πL}{12{t}_{0}}$;
(3)AC、AD边上可能有粒子射出的范围为CE段和DF段,${x}_{CE}=\frac{L}{4}$、${x}_{DF}=\frac{L}{2}$.
点评 本题考查了带电粒子在磁场中的运动,关键作出运动的轨迹,抓住临界状态,结合半径公式和周期公式进行求解,难度中等.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案科目:高中物理 来源: 题型:多选题
| A. | 小球刚好过最高点时的速度是$\sqrt{gR}$ | |
| B. | 小球过最高点时的最小速度是0 | |
| C. | 小球过最高点时,绳子张力可以为0 | |
| D. | 小球过最高点时,绳子对小球的作用力可以与所受的重力方向相反 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 在探究弹力和弹簧伸长量的关系时,某同学先按图1对弹簧甲进行探究,然后将弹簧乙和弹簧甲串联起来按图2进行探究.不考虑两个弹簧重力的影响,在弹性限度内,将质量m=50g的钩码逐个挂在弹簧下端,分别测得图1、图2中弹簧总长度L1、L2如表所示.
在探究弹力和弹簧伸长量的关系时,某同学先按图1对弹簧甲进行探究,然后将弹簧乙和弹簧甲串联起来按图2进行探究.不考虑两个弹簧重力的影响,在弹性限度内,将质量m=50g的钩码逐个挂在弹簧下端,分别测得图1、图2中弹簧总长度L1、L2如表所示.| 钩码个数 | 1 | 2 | 3 | 4 |
| L1/cm | 26.00 | 26.48 | 26.97 | 27.47 |
| L2/cm | 79.44 | 80.89 | 82.36 | 83.85 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,矩形ABCD位于匀强电场中,且与匀强电场方向平行.已知AB=2BC,A、B、D的电势分别为6V、2V、4V.初动能为24eV、电荷量大小为4e的带电粒子从A沿着AC方向射入电场,恰好经过B.不计粒子的重力,下列说法正确的是( )
如图所示,矩形ABCD位于匀强电场中,且与匀强电场方向平行.已知AB=2BC,A、B、D的电势分别为6V、2V、4V.初动能为24eV、电荷量大小为4e的带电粒子从A沿着AC方向射入电场,恰好经过B.不计粒子的重力,下列说法正确的是( )| A. | 该粒子一定带负电 | B. | 该粒子达到点B时的动能为40eV | ||
| C. | 改变初速度方向,该粒子可能经过C | D. | 改变初速度方向,该粒子可能经过D |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
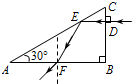 如图所示,直角棱镜ABC置于空气中,∠A=30°,AB边长为2a.一束单色光从D点垂直于BC边射入棱镜,在AC边上的E点恰好发生一次全反射后,从AB边中点F处射出.已知真空中光速为c.求:
如图所示,直角棱镜ABC置于空气中,∠A=30°,AB边长为2a.一束单色光从D点垂直于BC边射入棱镜,在AC边上的E点恰好发生一次全反射后,从AB边中点F处射出.已知真空中光速为c.求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题

| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
 一定质量的理想气体,由状态A通过如图所示的箭头方向变化到状态C.则气体由状态A到状态B的过程中,气体的内能不变(选填“增大”、“减小”或“不变”),气体由状态A到状态C的过程中,气体与外界总的热交换情况是放热(选填“吸热”、“放热”或“无法确定”)
一定质量的理想气体,由状态A通过如图所示的箭头方向变化到状态C.则气体由状态A到状态B的过程中,气体的内能不变(选填“增大”、“减小”或“不变”),气体由状态A到状态C的过程中,气体与外界总的热交换情况是放热(选填“吸热”、“放热”或“无法确定”)查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,半径为R的光滑圆形轨道竖直固定放置,小球a在圆形轨道内侧做圆周运动.对于半径R不同的圆形轨道,小球a通过轨道最高点时都恰好与轨道间没有相互作用力.下列说法中正确的是( )
如图所示,半径为R的光滑圆形轨道竖直固定放置,小球a在圆形轨道内侧做圆周运动.对于半径R不同的圆形轨道,小球a通过轨道最高点时都恰好与轨道间没有相互作用力.下列说法中正确的是( )| A. | 半径R越大,小球通过轨道最高点时的速度越大 | |
| B. | 半径R越大,小球通过轨道最高点时的角速度越小 | |
| C. | 半径R越大,小球通过轨道最高点时的向心加速度越大 | |
| D. | 半径R越大,小球通过轨道最高点时的向心力越大 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com