
分析 (1)以岸为参照物,根据位移与速度的比值为时间,结合题意,即可求解;
(2)根据垂直横渡正对岸,结合矢量的合成法则,及三角知识,即可求解.
解答 解:(1)以岸为参照物,
设AB相距x,水流速度v,甲船静水速度v1,乙船静水速度v2
由题意 $\frac{x}{{2({v_0}+{v_1})}}=\frac{x}{{2({v_2}-{v_0})}}=4$$\frac{{\frac{x}{2}+30}}{{{v_2}+{v_0}}}=\frac{{\frac{x}{2}-30}}{{{v_1}-{v_0}}}$
得:v0=$\frac{15}{4}$=3.75km/h
(2)甲船垂直横渡正对岸,对岸速度v1′=$\sqrt{{v}_{1}^{2}-{v}_{0}^{2}}$=$\frac{15\sqrt{3}}{4}$km/h
所需时间 ${t'_1}=\frac{L}{{{{v'}_1}}}=\frac{{8\sqrt{3}}}{45}≈0.31h$
乙船垂直横渡正对岸,船头与上游河岸的夹角满足cosα=$\frac{{v}_{0}}{{v}_{1}}$=$\frac{\frac{15}{4}}{15}$=$\frac{1}{4}$
答:(1)水流速度3.75km/h;
(2)该河流的河岸宽度为2km,当甲船以静水速度v1=7.5km/h,乙船以静水速度v2=15km/h分别垂直横渡到正对岸,甲船渡河所需的时间是0.31h;
乙船的船头与上游河岸的夹角的余弦值为$\frac{1}{4}$.
点评 考查运动的合成与分解,掌握矢量的合成法则的应用,注意区别最短时间与最短位移渡河的情况.


 口算能手系列答案
口算能手系列答案科目:高中物理 来源: 题型:解答题
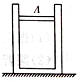 如图所示,开口向上竖直放置的内壁光滑导热良好的汽缸,内有质量为m的导热活塞,缸内密封着理想气体.初状态整个装置静止不动,气体的长度为l0=15cm,设外界大气压强为p0保持不变,温度为t0=27℃,活塞横截面积为S,且mg=p0S,求:
如图所示,开口向上竖直放置的内壁光滑导热良好的汽缸,内有质量为m的导热活塞,缸内密封着理想气体.初状态整个装置静止不动,气体的长度为l0=15cm,设外界大气压强为p0保持不变,温度为t0=27℃,活塞横截面积为S,且mg=p0S,求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
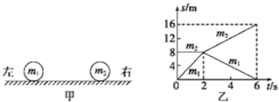
| A. | 碰前m2和m1都向右运动 | B. | 碰后m2和m1都向右运动 | ||
| C. | 由动量守恒可以算出m2=0.3kg | D. | 该碰撞为完全弹性碰撞 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
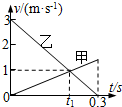 两物体甲和乙沿着同一条直线运动,t=0时,乙在甲的前方1m处.它们在0~0.3s时间内的v-t图象如图所示.若仅在两物体之间存在恒定的相互作用力,则( )
两物体甲和乙沿着同一条直线运动,t=0时,乙在甲的前方1m处.它们在0~0.3s时间内的v-t图象如图所示.若仅在两物体之间存在恒定的相互作用力,则( )| A. | 在t=0.3s后,乙将保持静止状态 | B. | 在t1时刻两者相距最近 | ||
| C. | 由图象可求t1=0.2s | D. | m甲:m乙=2:1 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
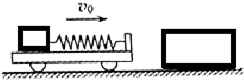 如图,水平面上有一质量m=10kg 的小车,其右端固定一水平轻质弹簧,弹簧左端连接一质量m0=10kg 的小物块,小物块与小车一起以v0=6m/s 的速度向右运动,与静止在水平面上质量M=40kg 的木箱发生正碰,碰后木箱的速度为v=2m/s,碰撞时间极短,弹簧始终在弹性限度内,忽略一切摩擦阻力.求:
如图,水平面上有一质量m=10kg 的小车,其右端固定一水平轻质弹簧,弹簧左端连接一质量m0=10kg 的小物块,小物块与小车一起以v0=6m/s 的速度向右运动,与静止在水平面上质量M=40kg 的木箱发生正碰,碰后木箱的速度为v=2m/s,碰撞时间极短,弹簧始终在弹性限度内,忽略一切摩擦阻力.求:查看答案和解析>>
科目:高中物理 来源: 题型:计算题
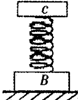 如图所示,质量为M=0.5kg的物体B和质量为m=0.2kg的物体C,用劲度系数为k=100N/m的轻弹簧连在一起.物体B放在水平地面上,物体C在轻弹簧的上方静止不动.现将物体C竖直向下缓慢压下一段距离x=0.03m后释放,物体C就上下做简谐运动,在运动过程中,物体B始终不离开地面.已知重力加速度大小为g=10m/s2.试求:当物体C运动到最高点时,物体C的加速度大小和此时物体B对地面的压力大小.
如图所示,质量为M=0.5kg的物体B和质量为m=0.2kg的物体C,用劲度系数为k=100N/m的轻弹簧连在一起.物体B放在水平地面上,物体C在轻弹簧的上方静止不动.现将物体C竖直向下缓慢压下一段距离x=0.03m后释放,物体C就上下做简谐运动,在运动过程中,物体B始终不离开地面.已知重力加速度大小为g=10m/s2.试求:当物体C运动到最高点时,物体C的加速度大小和此时物体B对地面的压力大小.查看答案和解析>>
科目:高中物理 来源: 题型:实验题
 小明同学看到一个纽扣锂电池标称电动势为3V,内阻约为1kΩ.为了较准确测定其电动势和内阻,除待测电池外,还备有如下器材:
小明同学看到一个纽扣锂电池标称电动势为3V,内阻约为1kΩ.为了较准确测定其电动势和内阻,除待测电池外,还备有如下器材:查看答案和解析>>
科目:高中物理 来源: 题型:计算题
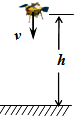 如图所示,“嫦娥三号”探测器在月球上着陆的最后阶段为:当探测器下降到距离月球表面高度为h时,探测器速度竖直向下,大小为v,此时关闭发动机,探测器仅在重力(月球对探测器的重力)作用下落到月面.已知从关闭发动机到探测器着地时间为t,月球半径为R且h<<R,引力常量为G,忽略月球自转影响,则:
如图所示,“嫦娥三号”探测器在月球上着陆的最后阶段为:当探测器下降到距离月球表面高度为h时,探测器速度竖直向下,大小为v,此时关闭发动机,探测器仅在重力(月球对探测器的重力)作用下落到月面.已知从关闭发动机到探测器着地时间为t,月球半径为R且h<<R,引力常量为G,忽略月球自转影响,则:查看答案和解析>>
科目:高中物理 来源: 题型:实验题
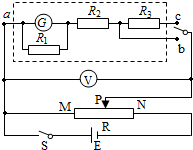 某同学改装和校准电压表的电路图如图所示,图中虚线框内是电压表的改装电路.
某同学改装和校准电压表的电路图如图所示,图中虚线框内是电压表的改装电路. 对改装表3V挡的不同刻度进行校准.所用电池的电动势E为5V;滑动变阻器R有两种规格,最大阻值分别为50Ω和5kΩ.为了方便实验中调节电压,图中R应选用最大阻值为50Ω的滑动变阻器.
对改装表3V挡的不同刻度进行校准.所用电池的电动势E为5V;滑动变阻器R有两种规格,最大阻值分别为50Ω和5kΩ.为了方便实验中调节电压,图中R应选用最大阻值为50Ω的滑动变阻器.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com