
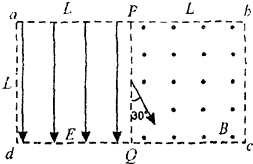
 如图所示,虚线框abcd内为边长均为L的正形匀强电场和匀强磁场区域,电场强度的大小为E,方向向下,磁感应强度为B,方向垂直纸面向外,PQ为其分界线,现有一群质量为m,电荷量为-e的电子(重力不计)从PQ中点与PQ成30°.角以不同的初速射入磁场,求:
如图所示,虚线框abcd内为边长均为L的正形匀强电场和匀强磁场区域,电场强度的大小为E,方向向下,磁感应强度为B,方向垂直纸面向外,PQ为其分界线,现有一群质量为m,电荷量为-e的电子(重力不计)从PQ中点与PQ成30°.角以不同的初速射入磁场,求:分析 (1)根据粒子在磁场中做圆周运动的圆心角,结合周期公式求出电子在磁场中运动的时间.
(2)电子在磁场中做匀速圆周运动,画出运动轨迹图,根据几何知识求半径和初速度v应满足的条件.
(3)电子在电场中做类平抛运动,电场力做功,由动能定理即可列式求解.
解答 解:(1)由洛仑兹力充当向心力:eBv=m$\frac{{v}^{2}}{r}$ ①
电子在磁场中运动的周期:T=$\frac{2πr}{v}$ ②
联立①②解得;T=$\frac{2πm}{qB}$.
能从PQ边进入电场(如图).粒子在匀强磁场中运动时间为t,由图知
t=$\frac{5}{6}$T ③
解得:t=$\frac{5πm}{3eB}$.
(2)当电子轨迹与Pb边相切时,有满足条件的最大速度v,由几何关系知其轨道半径r满足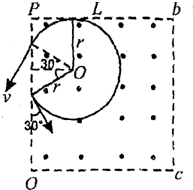
r+rsin30°=$\frac{L}{2}$ ④
解得r=$\frac{L}{3}$
洛仑兹力充当向心力:eBv=m$\frac{{v}^{2}}{r}$
联立①④解得v=$\frac{eBL}{2m(1+sin30°)}=\frac{eBL}{3m}$.
因此,当v≤$\frac{eBL}{3m}$时,电子在磁场运动有最长时间.
(3)以最大速度v进入电场,且从aP边飞出时电子有最大动能EKM,由动能定理:
eE($\frac{L}{2}-\frac{L}{3}$)=Ekm-$\frac{1}{2}m{v}^{2}$ ⑥
解得Ekm=$\frac{1}{6}eEL+\frac{{e}^{2}{B}^{2}{L}^{2}}{18m}$.
答:(1)能从PQ边离开磁场的电子在磁场运动的时间为$\frac{5πm}{3eB}$.
(2)若要电子在磁场运动时间最长,其初速v应满足的条件为v≤$\frac{eBL}{3m}$.
(3)最终从电场aP边界飞出虚线框所具有的动能为$\frac{1}{6}eEL+\frac{{e}^{2}{B}^{2}{L}^{2}}{18m}$.
点评 本题主要考查了带电粒子在混合场中运动的问题,要求同学们能正确分析粒子的受力情况,再通过受力情况分析粒子的运动情况,熟练掌握圆周运动及平抛运动的基本公式,难度适中.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:解答题
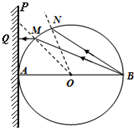 如图所示,一玻璃球体的半径为R,O为球心,AB为直径,在球的左侧有一竖直接收屏在A点与玻璃球相切.自B点发出的光线BM在M点射出,出射光线平行于AB,照射在接收屏上的Q点.另一光线BN恰好在N点发生全反射.已知∠ABM=30°,求
如图所示,一玻璃球体的半径为R,O为球心,AB为直径,在球的左侧有一竖直接收屏在A点与玻璃球相切.自B点发出的光线BM在M点射出,出射光线平行于AB,照射在接收屏上的Q点.另一光线BN恰好在N点发生全反射.已知∠ABM=30°,求查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 1.1×105Pa | B. | 3.0×105Pa | C. | 4.3×105Pa | D. | 1.2×106Pa |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
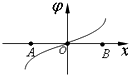 空间存在一沿x轴方向的静电场,电势φ随x变化的关系如图所示,图线关于坐标原点对称,A、B是x轴上关于原点对称的两点.下列说法中正确的是( )
空间存在一沿x轴方向的静电场,电势φ随x变化的关系如图所示,图线关于坐标原点对称,A、B是x轴上关于原点对称的两点.下列说法中正确的是( )| A. | O点处场强为零 | |
| B. | 电子在A、B两点的电场力大小相等,方向相反 | |
| C. | 电子在B点的电势能高于它在A点的电势能 | |
| D. | 电子从A点由静止释放后一直加速运动到B点 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com