
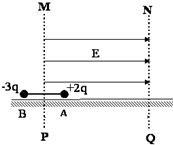
 如图所示,用长为L的绝缘轻杆连接两个质量均为m的带电小球A和B置于光滑绝缘的水平面上,A球的带电量为+2q,B球的带电量为-3q,构成一个带电系统(它们均可视为质点,也不考虑两者间相互作用的库仑力).现让小球A处在有界匀强电场区域内.已知虚线MP位于细杆的中垂线上,MP的左侧没有电场,右侧有匀强电场,电场强度大小为E,方向水平向右.从静止释放带电系统,(忽略带电系统运动过程中所产生的磁场影响).求:
如图所示,用长为L的绝缘轻杆连接两个质量均为m的带电小球A和B置于光滑绝缘的水平面上,A球的带电量为+2q,B球的带电量为-3q,构成一个带电系统(它们均可视为质点,也不考虑两者间相互作用的库仑力).现让小球A处在有界匀强电场区域内.已知虚线MP位于细杆的中垂线上,MP的左侧没有电场,右侧有匀强电场,电场强度大小为E,方向水平向右.从静止释放带电系统,(忽略带电系统运动过程中所产生的磁场影响).求:分析 (1)小球B刚进入电场带电系统具有最大速度,根据动能定理求出带电系统运动的最大速度;
(2)当带电系统速度第一次为零,B克服电场力做功最多,B增加的电势能最多,根据动能定理求出B运动的最大位移,结合电场力做功求出电势能增加量的最大值.
(3)根据牛顿第二定律,结合位移时间公式求出带电系统由静止释放到小球B刚进入电场的加速度,再根据牛顿第二定律和速度时间公式求出系统匀减速运动到零的时间,结合对称性求出带电系统回到初始位置时的加速度;由牛顿第二定律即可求出电量q.
解答 解:(1)小球B刚进入电场带电系统具有最大速度,从释放带电系统到小球B刚进入电场的过程中,根据动能定理有:$2qEL=\frac{1}{2}2mv_{max}^2-0$
整理得:${v_{max}}=\sqrt{\frac{2qEL}{m}}$.
(2)当带电系统速度第一次为零,B克服电场力做功最多,B增加的电势能最多
设B球在电场中的最大位移为x,由动能定理得:2qE(L+x)-3qEx=0-0
得:x=2L
所以B电势能增加的最大值为:W1=3qE×2L=6qEL
(3)设带电系统由静止释放到小球B刚进入电场的过程中,带电系统运动的时间为t,则有:$L=\frac{1}{2}{a}_{1}{t}^{2}$
其中:${a}_{1}=\frac{2qE}{2m}$,解得$t=\sqrt{\frac{2mL}{qE}}$
末速度v=a1t
又设小球B进入电场后至小球B出电场的过程中,带电系统运动的时间为t′,
其中:${a}_{2}=\frac{q′E-2qE}{2m}$
解得:$t′=\frac{2v}{{a}_{2}}$
根据对称性可知,带电系统从出电场到回到出发点的过程中所用的时间也是为t,而经时间t小球B进入电场,又经时间2t小球B第一次回到初始位置,所以:
t′=t
解得:q′=-6q.
答:(1)带电系统运动的最大速度为${v_{max}}=\sqrt{\frac{2qEL}{m}}$.
(2)带电系统运动过程中,B球电势能增加的最大值为6qEL;
(3)小球B的带电量q′为-6q.
点评 本题考查了动能定理和牛顿第二定律的综合,选择系统为研究对象,运用动能定理和牛顿第二定律进行求解,知道系统向右运动的过程和向左运动的过程具有对称性.


 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中物理 来源: 题型:计算题

查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,一U 形金属导轨竖直倒置,相距为L,磁感应强度的大小为B的匀强磁场与导轨平面垂直.一阻值为R、长度为L、质量为m的导体棒在距磁场上边界h处静止释放.导体棒进入磁场后速度减小,最终速度稳定时离磁场上边缘的距离为H.导体棒从静止开始运动到速度刚稳定的整个运动过程中,导体棒与导轨接触良好,且始终保持水平,不计导轨的电阻.下列说法正确的是( )
如图所示,一U 形金属导轨竖直倒置,相距为L,磁感应强度的大小为B的匀强磁场与导轨平面垂直.一阻值为R、长度为L、质量为m的导体棒在距磁场上边界h处静止释放.导体棒进入磁场后速度减小,最终速度稳定时离磁场上边缘的距离为H.导体棒从静止开始运动到速度刚稳定的整个运动过程中,导体棒与导轨接触良好,且始终保持水平,不计导轨的电阻.下列说法正确的是( )| A. | 整个运动过程中回路的最大电流为$\frac{{BL\sqrt{2gh}}}{R}$ | |
| B. | 整个运动过程中导体棒产生的焦耳热为mg(H+h)-$\frac{{{m^3}{g^2}{R^2}}}{{2{B^4}{L^4}}}$ | |
| C. | 整个运动过程中导体棒克服安培力所做的功为mgH | |
| D. | 整个运动过程中回路电流的功率为${({\frac{mg}{BL}})^2}R$ |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示,倾角θ=30°的光滑倾斜导体轨道(足够长)与光滑水平导体轨道连接,轨道宽度均为L=1m,电阻忽略不计.匀强磁场I仅分布在水平轨道平面所在区域,方向水平向右,大小B1=1T,匀强磁场II仅分布在倾斜轨道平面所在区域,方向垂直于倾斜轨道平面向下,大小B2=2T,现将两质量均为m=0.4kg,电阻均为R=0.5Ω的相同导体棒ab和cd,垂直于轨道分别置于水平轨道上和倾斜轨道上,并同时由静止释放,g=10m/s2.
如图所示,倾角θ=30°的光滑倾斜导体轨道(足够长)与光滑水平导体轨道连接,轨道宽度均为L=1m,电阻忽略不计.匀强磁场I仅分布在水平轨道平面所在区域,方向水平向右,大小B1=1T,匀强磁场II仅分布在倾斜轨道平面所在区域,方向垂直于倾斜轨道平面向下,大小B2=2T,现将两质量均为m=0.4kg,电阻均为R=0.5Ω的相同导体棒ab和cd,垂直于轨道分别置于水平轨道上和倾斜轨道上,并同时由静止释放,g=10m/s2.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
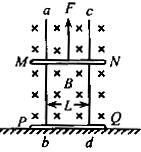 如图所示,两根竖直固定的足够长的金属导轨cd和ef相距L=0.2m,另外两根水平金属杆MN和PQ的质量均为m=2×10-2kg,可沿导轨无摩擦地滑动,MN杆和PQ杆的电阻均为R=0.1Ω(竖直金属导轨电阻不计),PQ杆放置在水平绝缘平台上,整个装置处于匀强磁场内,磁场方向垂直于导轨平面向里,磁感应强度B=1.0T.现让MN杆在恒定拉力作用下由静止开始向上加速运动,已知MN杆达到最大速度时,PQ杆对绝缘平台的压力恰好为零.(g取10m/s2)求:
如图所示,两根竖直固定的足够长的金属导轨cd和ef相距L=0.2m,另外两根水平金属杆MN和PQ的质量均为m=2×10-2kg,可沿导轨无摩擦地滑动,MN杆和PQ杆的电阻均为R=0.1Ω(竖直金属导轨电阻不计),PQ杆放置在水平绝缘平台上,整个装置处于匀强磁场内,磁场方向垂直于导轨平面向里,磁感应强度B=1.0T.现让MN杆在恒定拉力作用下由静止开始向上加速运动,已知MN杆达到最大速度时,PQ杆对绝缘平台的压力恰好为零.(g取10m/s2)求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
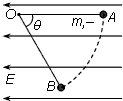 如图所示,在场强大小为E的匀强电场中,一根不可伸长的绝缘细线一端拴一个质量为m、电荷量为q的带负电小球,另一端固定在O点.把小球拉到使细线水平的位置A,然后将小球由静止释放,小球沿弧线运动到细线与水平成θ=60°的位置B时速度为零.以下说法正确的是( )
如图所示,在场强大小为E的匀强电场中,一根不可伸长的绝缘细线一端拴一个质量为m、电荷量为q的带负电小球,另一端固定在O点.把小球拉到使细线水平的位置A,然后将小球由静止释放,小球沿弧线运动到细线与水平成θ=60°的位置B时速度为零.以下说法正确的是( )| A. | 电场力与小球重力的关系是qE=mg | B. | 电场力与小球重力的关系是qE=$\sqrt{3}$mg | ||
| C. | 小球在B点时,细线拉力为FT=$\sqrt{3}$mg | D. | 小球在B点时,细线拉力为FT=$\frac{2\sqrt{3}}{3}$mg |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
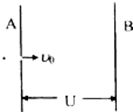 如图所示,A和B是置于真空中的两平行金属板,所加电压为U.一带负电的粒子以初速度v0由小孔水平射入电场中,粒子刚好能达到金属板.如果要使粒子刚好达到两板间距离的一半处,可采取的办法有( )
如图所示,A和B是置于真空中的两平行金属板,所加电压为U.一带负电的粒子以初速度v0由小孔水平射入电场中,粒子刚好能达到金属板.如果要使粒子刚好达到两板间距离的一半处,可采取的办法有( )| A. | 初速度为$\frac{{V}_{0}}{2}$,电压为$\frac{U}{2}$ | B. | 初速度为$\frac{{V}_{0}}{2}$,电压U不变 | ||
| C. | 初速度为V0,电压为$\frac{U}{2}$ | D. | 初速度为V0,电压为$\sqrt{2}$U |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
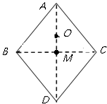 如图所示,在光滑绝缘水平面上,菱形ABCD边长为L,对角线BC长也为L,M为BC中点,O为三角形ABC的中心,现于B、C处各固定电量为+2Q的点电荷.下列说法正确的是( )
如图所示,在光滑绝缘水平面上,菱形ABCD边长为L,对角线BC长也为L,M为BC中点,O为三角形ABC的中心,现于B、C处各固定电量为+2Q的点电荷.下列说法正确的是( )| A. | A处与D处的场强相同 | |
| B. | 若再在A处固定电量为-Q的点电荷,则O处的场强大小为$\frac{9KQ}{{L}^{2}}$ | |
| C. | 若点电荷-Q从A静止释放,则经过M时速度最大 | |
| D. | 若点电荷+Q从B右侧靠近B的某点静止释放,沿BC向右运动过程加速度先增大后减小 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
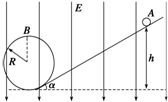 如图所示,在竖直向下的匀强电场中有一绝缘的光滑轨道,一个带负电的小球从斜轨道上的A点由静止释放,沿轨道下滑,已知小球的质量为m、电荷量为-q,匀强电场的场强大小为E,斜轨道的倾角为α(小球的重力大于所受的电场力)
如图所示,在竖直向下的匀强电场中有一绝缘的光滑轨道,一个带负电的小球从斜轨道上的A点由静止释放,沿轨道下滑,已知小球的质量为m、电荷量为-q,匀强电场的场强大小为E,斜轨道的倾角为α(小球的重力大于所受的电场力)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com