
| A. | $\frac{R-d}{R+h}$ | B. | $\frac{(R-d)^{2}}{(R+h)^{2}}$ | C. | $\frac{(R-d){(R+h)}^{2}}{{R}^{3}}$ | D. | $\frac{(R-d)(R+h)}{{R}^{2}}$ |
分析 根据题意知,地球表面的重力加速度等于半径为R的球体在表面产生的加速度,深度为d的地球内部的重力加速度相当于半径为R-d的球体在其表面产生的重力加速度,根据地球质量分布均匀得到加速度的表达式,再根据半径关系求解深度为d处的重力加速度与地面重力加速度的比值.卫星绕地球做圆周运动时,运用万有引力提供向心力可以解出高度为h处的加速度,再求其比值.
解答 解:令地球的密度为ρ,则在地球表面,重力和地球的万有引力大小相等,有:g=G$\frac{M}{{R}^{2}}$
由于地球的质量为:M=ρ•$\frac{4}{3}π{R}^{3}$,所以重力加速度的表达式可写成:g=$\frac{GM}{{R}^{2}}$=$\frac{G•ρ\frac{4}{3}π{R}^{3}}{{R}^{2}}$=$\frac{4}{3}$πGρR.
根据题意有,质量分布均匀的球壳对壳内物体的引力为零,固在深度为d的地球内部,受到地球的万有引力即为半径等于(R-d)的球体在其表面产生的万有引力,故井底的重力加速度g′=$\frac{4}{3}$πGρ(R-d).
所以有$\frac{g′}{g}=\frac{R-d}{R}$
根据万有引力提供向心力$G\frac{Mm}{{(R+h)}^{2}}=ma$,“天宫一号”的加速度为$a=\frac{GM}{(R+h)^{2}}$
所以$\frac{a}{g}=\frac{{R}^{2}}{(R+h)^{2}}$
所以$\frac{g′}{a}=\frac{(R-d){(R+h)}^{2}}{{R}^{3}}$,故C正确、ABD错误.
故选:C.
点评 抓住在地球表面重力和万有引力相等,在地球内部,地球的重力和万有引力相等,要注意在地球内部距离地面d处所谓的地球的质量不是整个地球的质量而是半径为(R-d)的球体的质量.


 阅读快车系列答案
阅读快车系列答案科目:高中物理 来源: 题型:解答题
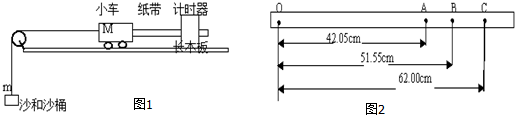
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
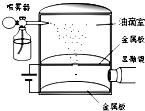 如图是密立根油滴实验的示意图.油滴从喷雾器的喷嘴喷出,落到图中的匀强电场中,调节两板间的电压,通过显微镜观察到某一油滴静止在电场中.下列说法正确的是( )
如图是密立根油滴实验的示意图.油滴从喷雾器的喷嘴喷出,落到图中的匀强电场中,调节两板间的电压,通过显微镜观察到某一油滴静止在电场中.下列说法正确的是( )| A. | 油滴带正电 | |
| B. | 油滴带负电 | |
| C. | 只要测出两板间的距离和电压就能求出油滴的电量 | |
| D. | 该实验测得油滴所带电荷量等于元电荷的整数倍 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,偏振片正对工作的液晶显示器,透过偏振片看到显示器亮度正常,将镜片转动90°,透过镜片看到的屏幕漆黑,则( )
如图所示,偏振片正对工作的液晶显示器,透过偏振片看到显示器亮度正常,将镜片转动90°,透过镜片看到的屏幕漆黑,则( )| A. | 显示器发出的光是纵波 | B. | 显示器发出的光是横波 | ||
| C. | 显示器发出的光是自然光 | D. | 显示器发出的光是偏振光 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
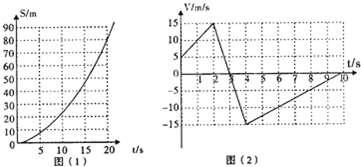
| A. | 由图(1)可知,质点做曲线运动,且速度逐渐增大 | |
| B. | 由图(1)可知,质点在前10s内的平均的速度大小为4m/s | |
| C. | 由图(2)可知,质点在第4s内加速度的方向与物体运动的方向相反 | |
| D. | 由图(2)可知,质点在运动过程中,加速度的最大值为15m/s2 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
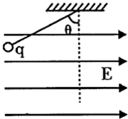 如图所示,一质量为m=1.0×10-2kg,带电量q=1.0×10-6C的小球,用绝缘细线悬挂在水平向右的匀强电场中,假设电场足够大,静止时悬线向左与竖直方向成θ=60°角.现突然将该电场方向变为竖直向上且大小不变,不考虑因电场的改变而带来的其他影响,小球在运动过程电量保持不变,重力加速度g=10m/s2,结果保留2位有效数字.
如图所示,一质量为m=1.0×10-2kg,带电量q=1.0×10-6C的小球,用绝缘细线悬挂在水平向右的匀强电场中,假设电场足够大,静止时悬线向左与竖直方向成θ=60°角.现突然将该电场方向变为竖直向上且大小不变,不考虑因电场的改变而带来的其他影响,小球在运动过程电量保持不变,重力加速度g=10m/s2,结果保留2位有效数字.查看答案和解析>>
科目:高中物理 来源: 题型:多选题
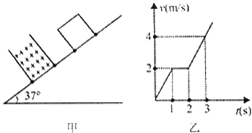 如图甲所示,倾角为37°的粗糙斜面上方有一垂直纸面向里,磁感应强度大小B=1T的有界匀强磁场区域.现有一正方形闭合线框从斜面上某处静止释放,线框共有n匝,电阻为10Ω,质量为2kg.线框的v-t图象如图乙所示,则下列说法正确的是(sin37°=0.6,cos37°=0.8)( )
如图甲所示,倾角为37°的粗糙斜面上方有一垂直纸面向里,磁感应强度大小B=1T的有界匀强磁场区域.现有一正方形闭合线框从斜面上某处静止释放,线框共有n匝,电阻为10Ω,质量为2kg.线框的v-t图象如图乙所示,则下列说法正确的是(sin37°=0.6,cos37°=0.8)( )| A. | 线框与斜面的动摩擦因数为0.5 | |
| B. | 线圈的匝数n=20 | |
| C. | 磁场的宽度为2m | |
| D. | 线圈通过磁场过程中产生的焦耳热为8J |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 2s末小球的动量大小为40kg•m/s | B. | 2s末小球的动能为40J | ||
| C. | 2s内重力的冲量大小为20N•s | D. | 2s内重力的平均功率为20W |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com