

分析 (1)根据实验的原理确定需要测量的物理量.
(2)根据动量守恒定律及机械能守恒定律可求得动量守恒及机械能守恒的表达式;
(3)小球落在斜面上,根据水平位移关系和竖直位移的关系,求出初速度与距离的表达式,从而得出动量守恒的表达式.
解答 解:(1)根据动量守恒得,m1•OP=m1•OM+m2•ON,所以除了测量线段OM、OP、ON的长度外,还需要测量的物理量是小球1和小球2的质量m1、m2.
故选:C.
(2)因为平抛运动的时间相等,则水平位移可以代表速度,OP是A球不与B球碰撞平抛运动的位移,该位移可以代表A球碰撞前的速度,OM是A球碰撞后平抛运动的位移,该位移可以代表碰撞后A球的速度,ON是碰撞后B球的水平位移,该位移可以代表碰撞后B球的速度,当所测物理量满足表达式m1•OP=m1•OM+m2•ON,说明两球碰撞遵守动量守恒定律,由功能关系可知,只要$\frac{1}{2}$m1v02=$\frac{1}{2}$m1v12+$\frac{1}{2}$m2v22成立则机械能守恒,故若m1•OP2=m1•OM2+m2•ON2,说明碰撞过程中机械能守恒.
(3)碰撞前,m1落在图中的P′点,设其水平初速度为v1.小球m1和m2发生碰撞后,m1的落点在图中M′点,设其水平初速度为v1′,m2的落点是图中的N′点,设其水平初速度为v2. 设斜面BC与水平面的倾角为α,
由平抛运动规律得:Lp′sinα=$\frac{1}{2}$gt2,Lp′cosα=v1t
解得v1=$\sqrt{\frac{g{L}_{P}co{s}^{2}α}{2sinα}}$.
同理v1′=$\sqrt{\frac{gL{′}_{M}co{s}^{2}α}{2sinα}}$,v2=$\sqrt{\frac{gL{′}_{N}co{s}^{2}α}{2sinα}}$,可见速度正比于$\sqrt{l}$.
所以只要验证m1$\sqrt{{l}_{2}}$=m1$\sqrt{{l}_{1}}$+m2$\sqrt{{l}_{3}}$ 即可.
故答案为.(1)C;(2)m1•OP=m1•OM+m2•ON m1•(OP)2=m1•(OM)2+m2•(ON)2;(3)m1$\sqrt{{l}_{2}}$=m1$\sqrt{{l}_{1}}$+m2$\sqrt{{l}_{3}}$
点评 解决本题的关键掌握实验的原理,以及实验的步骤,在验证动量守恒定律实验中,无需测出速度的大小,可以用位移代表速度.同时,在运用平抛运动的知识得出碰撞前后两球的速度,因为下落的时间相等,则水平位移代表平抛运动的速度.若碰撞前后总动能相等,则机械能守恒.


 优加精卷系列答案
优加精卷系列答案科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
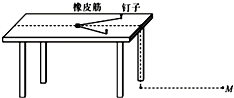 在验证机械能守恒定律实验时:
在验证机械能守恒定律实验时:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
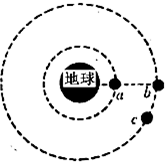 由中国航天科技集团公司五院自主研制的电推进系中2015年1月2日取得重要成果;电推进系统在试验中已突破6000小时,开关机3000次,具备确保该卫星在轨可靠运行15年的能力,如图所示为应用该系统的三颗卫星a、b、c绕地球做匀速圆周运动的示意图,其中b、c都在半径为r的轨道上,a是地球同步卫星,此时a、b恰好相距最近,已知地球质量为M,半径为R,地球自转的角速度为ω,万有引力常量为G,则( )
由中国航天科技集团公司五院自主研制的电推进系中2015年1月2日取得重要成果;电推进系统在试验中已突破6000小时,开关机3000次,具备确保该卫星在轨可靠运行15年的能力,如图所示为应用该系统的三颗卫星a、b、c绕地球做匀速圆周运动的示意图,其中b、c都在半径为r的轨道上,a是地球同步卫星,此时a、b恰好相距最近,已知地球质量为M,半径为R,地球自转的角速度为ω,万有引力常量为G,则( )| A. | 卫星b的周期小于24小时 | |
| B. | 卫星b和c的机械能相等 | |
| C. | 到卫星a和b下一次相距最近,还需经过时间t=$\frac{2π}{{ω-\sqrt{\frac{GM}{r^3}}}}$ | |
| D. | 卫星a的动能较大 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 王亚平在太空中授课过程中速度不变 | |
| B. | 王亚平相对机舱静止时对机舱的作用力为她的重力 | |
| C. | 飞船所在处的加速度为$\frac{GM}{(R+h)^{2}}$ | |
| D. | 飞船对地球的吸引力为G$\frac{Mm}{{R}^{2}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
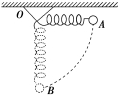 如图所示,一轻弹簧一端固定于O点,另一端系一重物,将重物从与悬点O在同一水平面且弹簧保持原长的A点无初速地释放,让它自由摆下,不计空气阻力,在重物由A点摆向B点的过程中( )
如图所示,一轻弹簧一端固定于O点,另一端系一重物,将重物从与悬点O在同一水平面且弹簧保持原长的A点无初速地释放,让它自由摆下,不计空气阻力,在重物由A点摆向B点的过程中( )| A. | 重力做正功,弹簧弹力不做功,弹性势能不变 | |
| B. | 重力做正功,弹簧弹力做负功,重力势能减小 | |
| C. | 重力不做功,弹簧弹力不做功,弹性势能不变 | |
| D. | 重力做正功,弹簧弹力做负功,弹性势能增加 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 它是人造地球卫星绕地球做圆周运动的最小运行速度 | |
| B. | 它是人造地球卫星绕地球做圆周运动的最大运行速度 | |
| C. | 它是近地圆形轨道上人造地球卫星的运行速度 | |
| D. | 它是发射卫星时的最小发射速度 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com