
| A. | 地球绕太阳运行的周期及地球离太阳的距离 | |
| B. | 月球绕地球运行的周期及月球离地球的距离 | |
| C. | 人造卫星在地面附近绕行的速度和运行周期 | |
| D. | 若不考虑地球自转,已知地球的半径及重力加速度 |
分析 地球、人造卫星等做匀速圆周运动,它们受到的万有引力充当向心力,用它们的运动周期表示向心力,由万有引力定律结合牛顿第二定律列式求中心天体的质量,然后由选项条件判断正确的答案.
解答 解:A、地球绕太阳运动的周期和地球与太阳的距离,根据万有引力提供向心力,其中地球质量在等式中消去,只能求出太阳的质量M.也就是说只能求出中心体的质量.故A错误.
B、地球对月球的万有引力提供向心力
$\frac{GmM}{{r}^{2}}$=m$\frac{{4π}^{2}}{{T}^{2}}$r,
月球绕地球运行的周期及月球离地球的距离,所以可以计算出地球质量,故B正确;
C、已知人造地球卫星在地面附近运行的速度v和运行周期T,依据$\frac{GmM}{{r}^{2}}$=$\frac{{mv}^{2}}{r}$,v=$\frac{2πr}{T}$可解得地球质量,故C正确.
D、已知地球半径R和地球表面重力加速度g,依据$\frac{G{Mm}_{0}}{{R}^{2}}$=m0g,可以解得地球质量,故D正确.
本题选不能计算出地球质量的,故选:A.
点评 解答万有引力定律在天体运动中的应用时要明确天体做匀速圆周运动,其受到的万有引力提供向心力,会用线速度、角速度、周期表示向心力,同时注意公式间的化简.


科目:高中物理 来源: 题型:解答题
 如图,一个质量为0.6kg 的小球以某一初速度从P点水平抛出,恰好从光滑圆弧ABC的A点的切线方向进入圆弧(不计空气阻力,进入圆弧时无机械能损失).已知圆弧的半径R=0.3m,θ=60°,小球到达A点时的速度 v=4m/s.(取g=10m/s2)求:
如图,一个质量为0.6kg 的小球以某一初速度从P点水平抛出,恰好从光滑圆弧ABC的A点的切线方向进入圆弧(不计空气阻力,进入圆弧时无机械能损失).已知圆弧的半径R=0.3m,θ=60°,小球到达A点时的速度 v=4m/s.(取g=10m/s2)求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 若使放射性物质的温度升高,其半衰期可能变小 | |
| B. | 玻尔将量子观念引入原子领域,其理论能够解释氢原子光谱的特征 | |
| C. | 氢原子的核外电子由离原子核较远的轨道跃迁到离核较近的轨道上时氢原子的能量减少 | |
| D. | 在原子核中,比结合能越小表示原子核中的核子结合得越牢固 | |
| E. | 一群处于n=4的激发态的氧原子,向低能级跃迁时,可能发射出的谱线为6条 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 做匀速圆周运动的物体必处于平衡状态 | |
| B. | 做匀速圆周运动的物体速度时刻改变,动能也时刻改变 | |
| C. | 做匀速圆周运动的物体合外力做功为零 | |
| D. | 做匀速圆周运动的物体的向心力是个恒力 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 力对物体做的功越多,力做功的功率越大 | |
| B. | 功率是描述物体做功快慢的物理量 | |
| C. | 从公式P=Fv可知,汽车的发动机功率可以随速度的不断增大而提高 | |
| D. | 当轮船航行时,如果牵引力与阻力相等时,合外力为零,所以此时发动机的实际功率为零 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 加速时做正功,匀速时不做功,减速时做负功 | |
| B. | 加速时做正功,匀速和减速时做负功 | |
| C. | 加速和匀速时做正功,减速时做负功 | |
| D. | 始终做正功 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 有向上的加速度和向下的速度 | B. | 有向下的加速度和向上的速度 | ||
| C. | 没有加速度,但有向上的速度 | D. | 没有加速度也没有速度 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
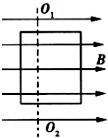 如图所示,在匀强磁场中匀速转动的矩形线圈的周期为T,转轴O1O2垂直于磁场方向,线圈电阻为2Ω.从线圈平面与磁场方向平行时开始计时,线圈转过60°时的感应电流为1A.那么( )
如图所示,在匀强磁场中匀速转动的矩形线圈的周期为T,转轴O1O2垂直于磁场方向,线圈电阻为2Ω.从线圈平面与磁场方向平行时开始计时,线圈转过60°时的感应电流为1A.那么( )| A. | 线圈消耗的电功率为2W | |
| B. | 线圈中感应电流的有效值为2A | |
| C. | 任意时刻线圈中的感应电动势为e=4cos$\frac{2π}{T}$t | |
| D. | 任意时刻穿过线圈的磁通量为φ=$\frac{T}{π}$sin$\frac{2π}{T}$t |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com