
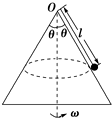
 如图所示,用一根长为l=1m的细线,一端系一质量为m=1kg的小球(可视为质点),另一端固定在一光滑锥体顶端,锥面与竖直方向的夹角θ=37°,当小球在水平面内绕锥体的轴做匀速圆周运动的角速度为ω时,细线的张力为T.(g取10m/s2,结果可用根式表示)求:
如图所示,用一根长为l=1m的细线,一端系一质量为m=1kg的小球(可视为质点),另一端固定在一光滑锥体顶端,锥面与竖直方向的夹角θ=37°,当小球在水平面内绕锥体的轴做匀速圆周运动的角速度为ω时,细线的张力为T.(g取10m/s2,结果可用根式表示)求:分析 (1)小球刚要离开锥面时的速度,此时支持力为零,根据牛顿第二定律求出该临界角速度ω0.
(2)若细线与竖直方向的夹角为60°时,小球离开锥面,由重力和细线拉力的合力提供向心力,运用牛顿第二定律求解.
解答  解:(1)若要小球刚好离开锥面,则小球受到重力和细线拉力如图所示.小球做匀速圆周运动的轨迹圆在水平面上,故向心力水平.
解:(1)若要小球刚好离开锥面,则小球受到重力和细线拉力如图所示.小球做匀速圆周运动的轨迹圆在水平面上,故向心力水平.
在水平方向运用牛顿第二定律及向心力公式得:
mgtan θ=mω${\;}_{0}^{2}$lsin θ
解得:ω${\;}_{0}^{2}$=$\frac{g}{lcosθ}$,即ω0=$\sqrt{\frac{g}{lcosθ}}$=$\sqrt{12.5}$ rad/s.
(2)同理,当细线与竖直方向成60°角时,由牛顿第二定律及向心力公式有:
mgtan α=mω′2lsin α
解得:ω′2=$\frac{g}{lcosα}$,即ω′=$\sqrt{\frac{g}{lcosθ}}$=$\sqrt{20}$=2$\sqrt{5}$ rad/s.
答:
(1)小球的角速度ω0至少为$\sqrt{12.5}$ rad/s.
(2)小球的角速度ω′为2$\sqrt{5}$ rad/s.
点评 本题的关键点在于判断小球是否离开圆锥体表面,不能直接应用向心力公式求解.


 阅读快车系列答案
阅读快车系列答案科目:高中物理 来源: 题型:选择题
 如图所示,真空中存在竖直向上的匀强电场和水平方向的匀强磁场.一质量为m,带电量为q的小球以速度v在竖直平面内做半径为R的匀速圆周运动,假设t=0时物体在轨迹最低点且重力势能为零,电势能也为零,下列说法正确的是( )
如图所示,真空中存在竖直向上的匀强电场和水平方向的匀强磁场.一质量为m,带电量为q的小球以速度v在竖直平面内做半径为R的匀速圆周运动,假设t=0时物体在轨迹最低点且重力势能为零,电势能也为零,下列说法正确的是( )| A. | 小球带负电 | |
| B. | 小球运动的过程中,机械能守恒,且机械能为E=$\frac{1}{2}$mv2 | |
| C. | 重力势能随时间的变化关系为Ep=mgRcos $\frac{v}{R}$t | |
| D. | 电势能随时间的变化关系为Ep′=mgR(cos $\frac{v}{R}$t-1) |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
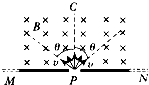 如图所示,在屏MN的上方有磁感应强度为B的匀强磁场,磁场的方向垂直纸面向里.P为屏上的一个小孔,PC与MN垂直.一群质量为m、带电量为q的粒子(不计重力),以相同的速率v,从P处沿垂直于磁场的方向射入磁场区域.粒子入射方向在与磁场B垂直的平面内,且散开在与PC夹角为θ的范围内,则在屏MN上被粒子打中的区域的长度为( )
如图所示,在屏MN的上方有磁感应强度为B的匀强磁场,磁场的方向垂直纸面向里.P为屏上的一个小孔,PC与MN垂直.一群质量为m、带电量为q的粒子(不计重力),以相同的速率v,从P处沿垂直于磁场的方向射入磁场区域.粒子入射方向在与磁场B垂直的平面内,且散开在与PC夹角为θ的范围内,则在屏MN上被粒子打中的区域的长度为( )| A. | $\frac{2mv(1-cosθ)}{qB}$ | B. | $\frac{2mv(1-sinθ)}{qB}$ | C. | $\frac{2mvcosθ}{qB}$ | D. | $\frac{2mv}{qB}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
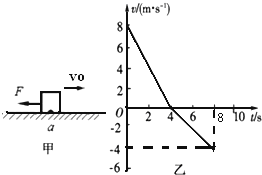 如图甲所示,质量m=4kg的物体在水平面上向右做直线运动.过a点时给物体作用一个水平向左的恒力F并开始计时,选水平向右为速度的正方向,通过速度传感器测出物体的瞬时速度,所得v-t图象如图乙所示.(取重力加速度为10m/s2)求:
如图甲所示,质量m=4kg的物体在水平面上向右做直线运动.过a点时给物体作用一个水平向左的恒力F并开始计时,选水平向右为速度的正方向,通过速度传感器测出物体的瞬时速度,所得v-t图象如图乙所示.(取重力加速度为10m/s2)求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
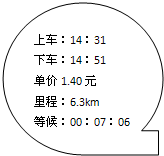
| A. | 14:31是时间 | B. | 14:51是时刻 | C. | 6.3km是位移 | D. | 00:07:06是时刻 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | $\frac{9F}{8}$ | B. | F | C. | $\frac{8F}{9}$ | D. | $\frac{2F}{3}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | tan2θ | B. | cotθ | C. | cot2θ | D. | 1+tan2θ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com