
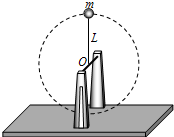
 如图所示,质量为M的支座上有一水平细轴,轴上套有一长为L的细绳,绳的另一端拴一质量为m可视为质点的小球.让小球在竖直面内做圆周运动.小球运动到最高点时底座对地面的压力恰仔为零.忽略一切阻力.运动过程中底座始终保持静止,重力加速度为g.则( )
如图所示,质量为M的支座上有一水平细轴,轴上套有一长为L的细绳,绳的另一端拴一质量为m可视为质点的小球.让小球在竖直面内做圆周运动.小球运动到最高点时底座对地面的压力恰仔为零.忽略一切阻力.运动过程中底座始终保持静止,重力加速度为g.则( )| A. | 运动过程中小球的最小速度为$\sqrt{\frac{MgL}{m}}$ | |
| B. | 运动过程中绳的最大拉力为6mg+Mg | |
| C. | 运动过程中小球的最大瞬时角速度为$\sqrt{\frac{(M+m)g}{mL}+\frac{2g}{L}}$ | |
| D. | 当绳处于水平时地面对底座的摩擦力为Mg+2mg |
分析 根据小球在最高点,底座对地面的压力为零,结合共点力平衡和牛顿第二定律求出小球的最小速度.根据动能定理和牛顿第二定律求出小球运动最低点的拉力,即最大拉力的大小.结合最大速度,结合线速度与角速度的关系求出最大瞬时角速度.根据动能定理和牛顿第二定律求出绳处于水平时绳子的拉力,结合平衡得出地面对底座的摩擦力.
解答 解:A、小球运动到最高点时,速度最小,在最高点,底座对地面的压力恰好为零,可知球对绳子的拉力等于Mg,根据牛顿第二定律得,F+mg=m$\frac{{v}^{2}}{L}$,解得最小速度v=$\sqrt{\frac{(M+m)gL}{m}}$,故A错误.
B、当小球运动到最低点时,拉力最大,根据动能定理得,$mg•2L=\frac{1}{2}mv{′}^{2}-\frac{1}{2}m{v}^{2}$,根据牛顿第二定律得,${F}_{m}-mg=m\frac{v{′}^{2}}{L}$,联立两式解得最大速度$v′=\sqrt{{v}^{2}+4gL}$,Fm=Mg+6mg,故B正确.
C、小球在运动过程中的最大瞬时角速度$ω=\frac{v′}{L}$=$\sqrt{\frac{(M+m)g}{mL}+\frac{4g}{L}}$,故C错误.
D、设绳处于水平时,小球的速度为v″,根据动能定理,$mgL=\frac{1}{2}mv{″}^{2}-\frac{1}{2}m{v}^{2}$,根据牛顿第二定律得,F=m$\frac{v{″}^{2}}{L}$,解得F=Mg+3mg,根据平衡知,地面对底座的摩擦力为Mg+3mg,故D错误.
故选:B.
点评 本题考查了牛顿第二定律、动能定理的综合运用,知道最低点的速度最大,抓住向心力的来源,结合牛顿第二定律进行求解,难度中等.


科目:高中物理 来源: 题型:实验题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
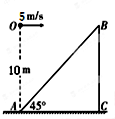 如图所示,斜面与水平面之间的夹角为45°,在斜面底端A点正上方高度为10m处的o点,以5m/s的速度水平抛出一个小球,飞行一段时间后撞在斜面上,这段飞行所用的时间为(g=10m/s2)( )
如图所示,斜面与水平面之间的夹角为45°,在斜面底端A点正上方高度为10m处的o点,以5m/s的速度水平抛出一个小球,飞行一段时间后撞在斜面上,这段飞行所用的时间为(g=10m/s2)( )| A. | 2s | B. | $\sqrt{2}$s | C. | 1s | D. | 0.5s |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
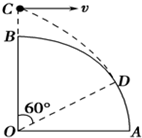 如图所示为四分之一圆柱体OAB的竖直截面,半径为R,在B点上方的C点水平抛出一个小球,小球轨迹恰好在D点与圆柱体相切,OD与OB的夹角为60°.求C点到B点的距离是多少?
如图所示为四分之一圆柱体OAB的竖直截面,半径为R,在B点上方的C点水平抛出一个小球,小球轨迹恰好在D点与圆柱体相切,OD与OB的夹角为60°.求C点到B点的距离是多少?查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 做曲线运动的物体受到的合外力可以为零 | |
| B. | 在恒力作用下,物体不可能做曲线运动 | |
| C. | 在变力作用下,物体一定做曲线运动 | |
| D. | 曲线运动一定是变速运动 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 汤姆生根据α粒子散射实验,提出了原子的葡萄干布丁模型 | |
| B. | 卢瑟福根据α粒子散射实验,提出了原子的核式结构模型 | |
| C. | 汤姆生最早发现电子 | |
| D. | 卢瑟福最早发现电子 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 同步卫星离地高度为$\root{3}{\frac{g{R}^{2}{T}^{2}}{2{π}^{2}}}$ | |
| B. | 同步卫星离地高度为$\root{3}{\frac{g{R}^{2}{T}^{2}}{4{π}^{2}}}$-R | |
| C. | t1=$\frac{T}{π}$arcsin$\root{3}{\frac{4{π}^{2}R}{g{T}^{2}}}$ | |
| D. | t1=$\frac{T}{2π}$arcsin$\root{3}{\frac{4{π}^{2}R}{g{T}^{2}}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com