
分析 (1)由质量守恒及电荷守恒写出核反应方程;
(2)由粒子做圆周运动,洛伦兹力做向心力求得运动周期,进而根据一个周期通过的电量为粒子所带电荷量得到等效电流;
(3)由(2)求得α粒子的速度,再通过动量守恒求得新核的速度,进而求得两粒子的动能,即可得到衰变过程的核能,再由爱因斯坦质能方程即可求得质量亏损.
解答 解:(1)由质量守恒及电荷守恒可得该α衰变的核反应方程为${\;}_{Z}^{A}X$→${\;}_{Z-2}^{A-4}Y$+${\;}_{2}^{4}H$;
(2)α粒子做圆周运动,洛伦兹力做向心力,设圆周运动的速率为v,则有:$Bvq=\frac{m{v}^{2}}{R}$,
则圆周运动的周期$T=\frac{2πR}{v}=\frac{2πm}{Bq}$;
那么相当于环形电流在周期T内通过的电量为q,则等效环形电流大小$I=\frac{q}{T}=\frac{B{q}^{2}}{2πm}$;
(3)因为衰变时间极短,且衰变时内力远远大于外力,故认为在衰变过程中外力可忽略,则有动量守恒,设新核的速度为v′,则有:mv+Mv′=0;
由(2)可得:$v=\frac{BqR}{m}$,所以,$v′=-\frac{BqR}{M}$,则衰变过程使两粒子获得动能$E=\frac{1}{2}m{v}^{2}+\frac{1}{2}Mv{′}^{2}$=$\frac{(BqR)^{2}}{2m}+\frac{(BqR)^{2}}{2M}=(\frac{1}{m}+\frac{1}{M})\frac{(BqR)^{2}}{2}$;
由于衰变过程,质量亏损产生的核能全部转化为粒子的动能,故衰变过程的质量亏损$△m=\frac{E}{{c}^{2}}=(\frac{1}{m}+\frac{1}{M})\frac{(BqR)^{2}}{2{c}^{2}}$;
答:(1)放射性原子核用${\;}_{Z}^{A}X$表示,新核的元素符号用Y表示,则该α衰变的核反应方程为${\;}_{Z}^{A}X$→${\;}_{Z-2}^{A-4}Y$+${\;}_{2}^{4}H$;
(2)α粒子的圆周运动可以等效成一个环形电流,则圆周运动的周期为$\frac{2πm}{Bq}$,环形电流大小为$\frac{B{q}^{2}}{2πm}$;
(3)设该衰变过程释放的核能都转为为α粒子和新核的动能,新核的质量为M,则衰变过程的质量亏损△m为损$(\frac{1}{m}+\frac{1}{M})\frac{(BqR)^{2}}{2{c}^{2}}$.
点评 带电粒子在磁场中的运动,一般由洛伦兹力做向心力,进而求得速度、半径、周期等问题,然后根据几何关系求得粒子运动轨迹,进而求解.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中物理 来源: 题型:计算题
 如图1所示,两物块A、B套在水平粗糙的CD杆上,并用不可伸长的轻绳连接,整个装置能绕过CD中点的轴OO1转动,已知两物块质量相等均为m,杆CD对物块A、B的最大静摩擦力大小相等且动摩擦系数为μ.开始时绳子处于自然长度(绳子恰好伸直但无弹力),物块B到OO1轴的距离为2L,物块A到OO1轴的距离为L,现让该装置从静止开始转动,使转速逐渐增大,求:
如图1所示,两物块A、B套在水平粗糙的CD杆上,并用不可伸长的轻绳连接,整个装置能绕过CD中点的轴OO1转动,已知两物块质量相等均为m,杆CD对物块A、B的最大静摩擦力大小相等且动摩擦系数为μ.开始时绳子处于自然长度(绳子恰好伸直但无弹力),物块B到OO1轴的距离为2L,物块A到OO1轴的距离为L,现让该装置从静止开始转动,使转速逐渐增大,求:查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示,质量为2m的小车静止于光滑的水平面上,小车AB段是半径为R的四分之一圆弧光滑轨道,BC段是长为是1.5R的水平粗糙轨道,两段轨道相切于B点,一质量为m的滑块在小车上从A点静止开始沿轨道下滑,重力加速度为g.
如图所示,质量为2m的小车静止于光滑的水平面上,小车AB段是半径为R的四分之一圆弧光滑轨道,BC段是长为是1.5R的水平粗糙轨道,两段轨道相切于B点,一质量为m的滑块在小车上从A点静止开始沿轨道下滑,重力加速度为g.查看答案和解析>>
科目:高中物理 来源: 题型:计算题
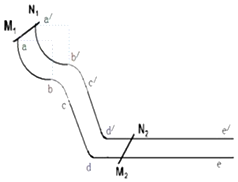 如图所示,竖直放置的平行导轨由四部分组成,其中只有水平部分是导体材料做的,其余部分均为绝缘材料,整个轨道处在竖直向上的匀强磁场中(磁场未画出).ab、a'b'是四分之一光滑圆弧形轨道,下端切线水平;bc、b'c'是抛物线轨道,cd、c'd'是倾斜轨道,de、d'e'是光滑水平轨道(足够长).倾斜轨道与水平轨道平滑连接.金属棒过dd'前后的速度大小不变,金属杆M1N1从静止开始沿轨道顶端aa'下滑,与抛物线轨道恰好无相互作用力并且恰好沿着倾斜轨道匀速滑下,之后进入水平轨道(0水平轨道上原来放有一根金属杆M2N2),在运动过程中两杆始终与导轨垂直并接触良好.已知圆弧半径为R=0.2m,M1N1的质量为m=1kg,M2N2的质量为2m,cd、c'd'倾斜轨道倾角θ=53°(sin53°=0.8,cos53°=0.6),cd、c'd'倾斜轨道长度s=0.5m,取重力加速度大小g=10m/s2.求:
如图所示,竖直放置的平行导轨由四部分组成,其中只有水平部分是导体材料做的,其余部分均为绝缘材料,整个轨道处在竖直向上的匀强磁场中(磁场未画出).ab、a'b'是四分之一光滑圆弧形轨道,下端切线水平;bc、b'c'是抛物线轨道,cd、c'd'是倾斜轨道,de、d'e'是光滑水平轨道(足够长).倾斜轨道与水平轨道平滑连接.金属棒过dd'前后的速度大小不变,金属杆M1N1从静止开始沿轨道顶端aa'下滑,与抛物线轨道恰好无相互作用力并且恰好沿着倾斜轨道匀速滑下,之后进入水平轨道(0水平轨道上原来放有一根金属杆M2N2),在运动过程中两杆始终与导轨垂直并接触良好.已知圆弧半径为R=0.2m,M1N1的质量为m=1kg,M2N2的质量为2m,cd、c'd'倾斜轨道倾角θ=53°(sin53°=0.8,cos53°=0.6),cd、c'd'倾斜轨道长度s=0.5m,取重力加速度大小g=10m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
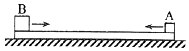 如图,两个滑块A和B的质量分别为mA=1kg和mB=5kg,放在静止与水平地面上的木板的两端,两者与木板间的动摩擦因数均为μ1=0.5;木板的质量为m=4kg,与地面间的动摩擦因数为μ2=0.1.某时刻A、B两滑块开始相向滑动,初速度大小均为v0=3m/s.A、B相遇时,A与木板恰好相对静止.设最大静摩擦力等于滑动摩擦力,取重力加速度大小g=10m/s2.求
如图,两个滑块A和B的质量分别为mA=1kg和mB=5kg,放在静止与水平地面上的木板的两端,两者与木板间的动摩擦因数均为μ1=0.5;木板的质量为m=4kg,与地面间的动摩擦因数为μ2=0.1.某时刻A、B两滑块开始相向滑动,初速度大小均为v0=3m/s.A、B相遇时,A与木板恰好相对静止.设最大静摩擦力等于滑动摩擦力,取重力加速度大小g=10m/s2.求查看答案和解析>>
科目:高中物理 来源: 题型:选择题

| A. | 该简谐波是纵波 | B. | 该简谐波的最大波长为2L | ||
| C. | t=$\frac{T}{8}$时,P在平衡位置上方 | D. | t=$\frac{3T}{8}$时,P的速度方向竖直向上 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
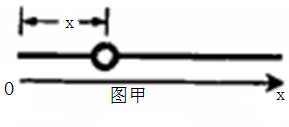 如图甲所示,光滑的绝缘细杆水平放置,有孔小球套在杆上,整个装置固定于某一电场中.以杆左端为原点,沿杆向右为x轴正方向建立坐标系.沿杆方向电场强度E随位置x的分布如图乙所示,场强为正表示方向水平向右,场强为负表示方向水平向左.图乙中曲线在0≤x≤0.20m和x≥0.4m范围可看作直线.小球质量m=0.02kg,带电量q=+1×10-6C.若小球在x2处获得一个v=0.4m/s的向右初速度,最远可以运动到x4处.
如图甲所示,光滑的绝缘细杆水平放置,有孔小球套在杆上,整个装置固定于某一电场中.以杆左端为原点,沿杆向右为x轴正方向建立坐标系.沿杆方向电场强度E随位置x的分布如图乙所示,场强为正表示方向水平向右,场强为负表示方向水平向左.图乙中曲线在0≤x≤0.20m和x≥0.4m范围可看作直线.小球质量m=0.02kg,带电量q=+1×10-6C.若小球在x2处获得一个v=0.4m/s的向右初速度,最远可以运动到x4处.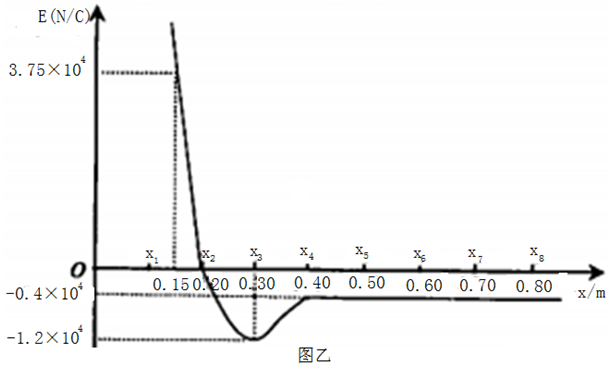 (3)若已知小球在x2处以初速度v0向左减速运动,速度减为零后又返回x2处,所用总时间为t0,求小球在x2处以初速度4v0向左运动,再返回到x2处所用的时间.(小球运动过程中始终未脱离杆)你可能不会计算,但小球向左运动过程中受力特点你并不陌生,请展开联想,通过类比分析得出结果.
(3)若已知小球在x2处以初速度v0向左减速运动,速度减为零后又返回x2处,所用总时间为t0,求小球在x2处以初速度4v0向左运动,再返回到x2处所用的时间.(小球运动过程中始终未脱离杆)你可能不会计算,但小球向左运动过程中受力特点你并不陌生,请展开联想,通过类比分析得出结果.查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 饱和气压与热力学温度成正比 | |
| B. | 一定量的理想气体在等温膨胀过程中吸收的热量等于对外做的功,并不违反热力学第二定律 | |
| C. | 当分子间的引力与斥力平衡时,分子力一定为零,分子势能一定最小 | |
| D. | 气体温度越高,气体分子运动越剧烈、容器壁受到的冲击力越大、气体的压强越大 | |
| E. | 在任何自然过程中,一个孤立系统中的总熵不会减少 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com