
 ��ͼ��ʾ��������е���ֱƽ���ڣ��ó�Ϊ2L�ľ�Ե�����������������Ϊm�Ĵ���С��A��B��A��ĵ����Ϊ+4q��B��ĵ����Ϊ-3q�����һ����ϵͳ������MN��PQƽ�У���ʼʱPQǡΪ�˵��д��ߣ���MN��PQ�����ֱ���ϵ���ǿ�糡��ǡ��ʹ����ϵͳ��ֹ��������ʹ�糡ǿ��ͻȻ�ӱ�����֪�����������ٶ�Ϊg������
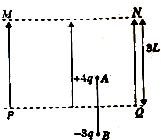
��ͼ��ʾ��������е���ֱƽ���ڣ��ó�Ϊ2L�ľ�Ե�����������������Ϊm�Ĵ���С��A��B��A��ĵ����Ϊ+4q��B��ĵ����Ϊ-3q�����һ����ϵͳ������MN��PQƽ�У���ʼʱPQǡΪ�˵��д��ߣ���MN��PQ�����ֱ���ϵ���ǿ�糡��ǡ��ʹ����ϵͳ��ֹ��������ʹ�糡ǿ��ͻȻ�ӱ�����֪�����������ٶ�Ϊg���������� ��1������ϵͳ��ֹʱ��A���ܵĵ糡����������ƽ�⣬�ɶ���ƽ��ó��糡ǿ�ȵı���ʽ���糡ǿ��ͻȻ�ӱ���ϵͳ�������ȼ���ֱ���˶����糡����A���������������������ɶ��ܶ������B��ս���糡ʱ���ٶ�v1�Ĵ�С��
��2�����˶�ȫ�̣�����������������ö��ܶ�����ʽ��⼴�ɣ�
��3��ϵͳ�����˶���Ϊ���Σ���һ���ȼ����˶�����ϵͳ��ʼ�����˶���B��ս���糡���̣�ϵͳ���ȼ���ֱ���˶�����ţ�ٵڶ�����������ٶȣ��ɳ��ٶ�0��ĩ�ٶ�v1�����ٶȹ�ʽ����˶���ʱ�䣮�ڶ����ȼ����˶�����B�����糡��A�ճ��糡��ϵͳ���ȼ���ֱ���˶����˹���ͨ����λ�Ƶ���L����ţ�ٶ���������ٶȣ����˶�ѧ��ʽ����˹����˶���ʱ�䣻�������ȼ����˶���A���糡��ϵͳ���ȼ���ֱ���˶�����ţ�ٶ���������ٶȣ����˶�ѧ��ʽ����˹����˶���ʱ�䣬��������ʱ�䣮
��� �⣺��1�������ϵͳ��ֹʱ�糡ǿ��ΪE������2mg=4qE����ã�
E=$\frac{mg}{2q}$ ��
�糡ǿ�ȼӱ���ϵͳ�ӿ�ʼ��ֹ��B����糡�����ݶ��ܶ����У�
��2E��4q-2mg��L=$\frac{1}{2}$��2m${v}_{1}^{2}$ ��
�����٢ڵ�B��ս���糡ʱ���ٶȣ�
${v}_{1}=\sqrt{2gL}$
��2����MN��PQ���ΪxʱA��ǡ�õ���糡�߽�MN�����ݶ��ܶ����õ���
2E•4q•��x-L��-2E•3q•��x-2L��-2mg��x-L��=0
��ã�
x=4L
��3������ϵͳ�������̺��½����̾��жԳ��ԣ�
����ϵͳ�����˶���Ϊ���Σ�
��һ���ȼ����˶�������ţ�ٵڶ������У�
a1=$\frac{8qE-2mg}{2m}$=g��
�˶�ʱ�䣺
t1=$\frac{{v}_{1}}{{a}_{1}}$=$\sqrt{\frac{2L}{g}}$��
�ڶ����ȼ����˶���ͬ���ɵã�
a2=$\frac{2mg+6qE-8qE}{2m}$=$\frac{g}{2}$
��A����糡ʱ�ٶ�Ϊv2�������˶�ѧ��ʽ�У�v22-v12=-2a2L��
���v2=$\sqrt{gL}$��
t2=$\frac{{v}_{2}-{v}_{1}}{{a}_{2}}$=2��$\sqrt{2}$-1��$\sqrt{\frac{L}{g}}$��
�������ȼ����˶���a3=$\frac{2mg+6qE}{2m}$=$\frac{5}{2}g$��t3=$\frac{{v}_{2}}{{a}_{3}}$=$\frac{2}{5}\sqrt{\frac{L}{g}}$
���˶�����T=2��t1+t2+t3��=��6$\sqrt{2}$-$\frac{16}{5}$��$\sqrt{\frac{L}{g}}$
�𣺣�1��B��յ���糡�߽�PQʱ���ٶȴ�СΪ$\sqrt{2gL}$��
��2����ҪʹA���뿪�糡�ϱ߽�MN����MN��PQ֮���������Ϊ4L��
��3������ϵͳ�˶�������Ϊ��6$\sqrt{2}$-$\frac{16}{5}$��$\sqrt{\frac{L}{g}}$��
���� �����ǵ糡����ѧ���ۺ��⣬�Ƚϸ��ӣ��ؼ����ڷ�������ϵͳ�������������ȷ���˶�����������ۺ�Ӧ�õ糡֪ʶ����ѧ֪ʶ��������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ���϶����š��������е����ڱȡ��϶���š��� | |
| B�� | ���϶����š��������е��ٶȱȡ��϶���š�С | |
| C�� | ���϶����š���������ʱ���ļ��ٶȱȡ��϶���š��� | |
| D�� | ���϶����š���������ʱ���ٶȱȡ��϶���š�С |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
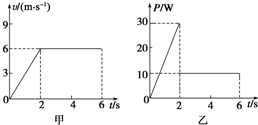 ���ڴֲ�ˮƽ���ϵ������ܵ�ˮƽ���������ã���0��6s�����ٶ���ʱ���ͼ��������Ĺ�����ʱ���ͼ��ֱ���ͼ�ס�����ʾ������˵����ȷ���ǣ�������
���ڴֲ�ˮƽ���ϵ������ܵ�ˮƽ���������ã���0��6s�����ٶ���ʱ���ͼ��������Ĺ�����ʱ���ͼ��ֱ���ͼ�ס�����ʾ������˵����ȷ���ǣ�������| A�� | 0��6s�������λ�ƴ�СΪ30m | |
| B�� | 0��6s���������Ĺ�Ϊ60J | |
| C�� | ��������0��6s��������0��2s��������� | |
| D�� | ����Ħ�����Ĵ�СΪ5N |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
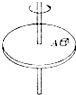
| A�� | ���� | B�� | ֧���� | ||
| C�� | ֧������Ħ�����ĺ��� | D�� | ָ��Բ�ĵ�Ħ���� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | �����ں��������£�һ����ֱ���˶� | |
| B�� | ������ʼ�����ٶȴ�ֱ�Ҵ�С������������£�һ��������Բ���˶� | |
| C�� | �����ڱ��������²�����������Բ���˶� | |
| D�� | �����ں��������£���������Բ���˶� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����

| A�� | �պϿ���kʱ��ͭ��Q���������ƶ� | |
| B�� | �պϿ���kʱ��ͭ��Q���ܲ����������ܵ������Ħ���� | |
| C�� | �ڿ���k�պϵ�����£������ƶ���ƬPʱ��ͭ��Qһ�������ƶ� | |
| D�� | �ڿ���k�պϵ�����£������ƶ���ƬPʱ��ͭ��Q���������ƶ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ��B��ϸ��ϵס��C��B֮��Ķ�Ħ�������̿���һ����Χ�ڱ仯��A������B�ϣ�A��Bʼ�����б�澲ֹ����ʼʱ��=0������Ħ�������������ֵʱ��A��B�����ĸ����ֱ�Ϊ��������
��ͼ��ʾ��B��ϸ��ϵס��C��B֮��Ķ�Ħ�������̿���һ����Χ�ڱ仯��A������B�ϣ�A��Bʼ�����б�澲ֹ����ʼʱ��=0������Ħ�������������ֵʱ��A��B�����ĸ����ֱ�Ϊ��������| A�� | 3����4�� | B�� | 3����5�� | C�� | 3����6�� | D�� | 4����3�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
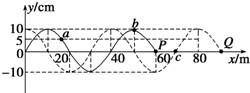 һ�м�г�Შ��x����������tʱ�̲���ͼ��ͼ�е�ʵ����ʾ����ʱ���պô���P�㣬t+0.6sʱ�̵IJ�����ͼ�е�������ʾ��a��b��c��P��Q�ǽ����е��ʵ㣬������˵����ȷ���ǣ�������
һ�м�г�Შ��x����������tʱ�̲���ͼ��ͼ�е�ʵ����ʾ����ʱ���պô���P�㣬t+0.6sʱ�̵IJ�����ͼ�е�������ʾ��a��b��c��P��Q�ǽ����е��ʵ㣬������˵����ȷ���ǣ�������| A�� | ���в��IJ��ٿ���Ϊ50m/s | |
| B�� | ��t+0.6 sʱ�̿�ʼ������0.5T���ʵ�b��x���������˶�20m | |
| C�� | �ʵ�c�����ʱ����ͨ����·�̿���Ϊ60 cm | |
| D�� | ��T=0.8s����t+0.5sʱ�̣��ʵ�b��P��λ����ͬ | |
| E�� | ��T=0.8s����t+0.4sʱ�̿�ʼ��ʱ�����ʵ�c������Ϊy=0.1sin��$\frac{5}{2}$��t����m�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com