
 ��ͼ��ʾ��������ȫ��ͬ�Ŀ���Ϊ�ʵ�����A��B������һ��ֹ��ˮƽ���ϵ���ճ����������ΪM��O�����ˮƽ��⻬���Ҳ�ˮƽ���ֲڣ�A��B��ֲ�ˮƽ���Ķ�Ħ��������Ϊ�̣�һ������Ϊm���ٶ�Ϊv0���ӵ�ˮƽ����A�����B�����ͣ��B�У��乲ͬ�ٶ�Ϊv���ӵ���B����O��ǰ����Ծ�ֹ����
��ͼ��ʾ��������ȫ��ͬ�Ŀ���Ϊ�ʵ�����A��B������һ��ֹ��ˮƽ���ϵ���ճ����������ΪM��O�����ˮƽ��⻬���Ҳ�ˮƽ���ֲڣ�A��B��ֲ�ˮƽ���Ķ�Ħ��������Ϊ�̣�һ������Ϊm���ٶ�Ϊv0���ӵ�ˮƽ����A�����B�����ͣ��B�У��乲ͬ�ٶ�Ϊv���ӵ���B����O��ǰ����Ծ�ֹ�������� ��i���ӵ��������ɵ�ϵͳ�����غ㣬�ɶ����غ㶨�ɿ�������ӵ����ٶȣ�
��ii����A��BӦ�ö��ܶ��������λ�ƣ�Ȼ�����A��Bֹͣ�˶�ʱ����ľ��룮
��� �⣺��i���ӵ���A��ɵ�ϵͳ�����غ㣬�ӵ���B��ɵ�ϵͳ�����غ㣬
������Ϊ�������ɶ����غ㶨�ɵã�
���ӵ���A��mv0=mv�ӵ�+2MvA��
���ӵ���B��mv�ӵ�+MvA=��m+M��v��
��ã�v�ӵ�=$\frac{2��M+m��v}{m}$-v0��vA=$\frac{m{v}_{0}-��M+m��v}{M}$��
��2���ɶ��ܶ����ã�
��A��-��MgsA=0-$\frac{1}{2}$MvA2��
���ӵ���B��-�̣�M+m��gsB=0-$\frac{1}{2}$��M+m��v2��
����ľ��룺d=sB-sA��
��ã�d=$\frac{{v}^{2}}{2��g}$-$\frac{[m{v}_{0}-��M+m��v]^{2}}{2��g{M}^{2}}$��
�𣺣�i���ӵ�����Aʱ���ٶ�Ϊ$\frac{2��M+m��v}{m}$-v0��
��ii��A��B�����ֹͣ�˶�ʱ֮��ľ���Ϊ$\frac{{v}^{2}}{2��g}$-$\frac{[m{v}_{0}-��M+m��v]^{2}}{2��g{M}^{2}}$��
���� ���⿼�������ٶȡ��������⣬�������������˶����̣�Ӧ�ö����غ㶨�ɡ����ܶ���������ȷ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
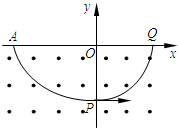 ��ͼ��ʾ��ֱ������ϵxOyλ����ֱƽ���ڣ�y����ֱ���ϣ��ڢ��������д�ֱ���������������ǿ�ų����ڢ�����ͬʱ���ڷ���ƽ����y�����ǿ�糡��ͼ��δ��������һ����С���x���ϵ�A���ɾ�ֹ�ͷţ�ǡ�ô�P�㴹ֱ��y�����ڢ����ޣ�Ȼ����Բ���˶�����Q�㴹ֱ��x�����ڢ����ޣ�Q���O��ľ���Ϊd���������ٶ�Ϊg������������Ϣ������������������У�������
��ͼ��ʾ��ֱ������ϵxOyλ����ֱƽ���ڣ�y����ֱ���ϣ��ڢ��������д�ֱ���������������ǿ�ų����ڢ�����ͬʱ���ڷ���ƽ����y�����ǿ�糡��ͼ��δ��������һ����С���x���ϵ�A���ɾ�ֹ�ͷţ�ǡ�ô�P�㴹ֱ��y�����ڢ����ޣ�Ȼ����Բ���˶�����Q�㴹ֱ��x�����ڢ����ޣ�Q���O��ľ���Ϊd���������ٶ�Ϊg������������Ϣ������������������У�������| A�� | Բ���˶����ٶȴ�С | B�� | �糡ǿ�ȵĴ�С�ͷ��� | ||
| C�� | С���ڵڢ������˶���ʱ�� | D�� | �Ÿ�Ӧǿ�ȴ�С |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ����L=31cm���ھ����ȵ�ϸ�����ܣ�����������ֱ���ã����ˮ������סL1=10cm���Ŀ��������ֽ��������Ե�Ϊ������ֱƽ���ڻ���ת��һ�ܣ�ֱ�������ٴ����ϣ������ܳ����ٴ�����ʱ�������ij��ȣ�������ѹǿP0=75cmHg��
��ͼ��ʾ����L=31cm���ھ����ȵ�ϸ�����ܣ�����������ֱ���ã����ˮ������סL1=10cm���Ŀ��������ֽ��������Ե�Ϊ������ֱƽ���ڻ���ת��һ�ܣ�ֱ�������ٴ����ϣ������ܳ����ٴ�����ʱ�������ij��ȣ�������ѹǿP0=75cmHg���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
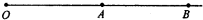 �����·��ʪ���������ǵij��кͽ�ͨ������������Ӱ�죬��֪������̥��������·��Ķ�Ħ������Ϊ��1�������ʪ���İ���·��Ķ�Ħ������Ϊ��2���������Գ��ٶ�v0�ظ���ˮƽ����·����ʻʱ������A����ɲ����ɲ����������ֹͣת����������Ҫ����һ�ξ��뵽B������ͣ�£�����������ͬ�����ٶ�v0�ڸ���ˮƽ����·��OA����ʻ��ͻȻ����ǰ����A����ʼ·����ˮʪ��������B�������ϰ��������ͣ������ͼ��ʾ����ʹ������ײ���ϰ������������Ӧ�ھ�A���Զ����ʼ��ɲ����
�����·��ʪ���������ǵij��кͽ�ͨ������������Ӱ�죬��֪������̥��������·��Ķ�Ħ������Ϊ��1�������ʪ���İ���·��Ķ�Ħ������Ϊ��2���������Գ��ٶ�v0�ظ���ˮƽ����·����ʻʱ������A����ɲ����ɲ����������ֹͣת����������Ҫ����һ�ξ��뵽B������ͣ�£�����������ͬ�����ٶ�v0�ڸ���ˮƽ����·��OA����ʻ��ͻȻ����ǰ����A����ʼ·����ˮʪ��������B�������ϰ��������ͣ������ͼ��ʾ����ʹ������ײ���ϰ������������Ӧ�ھ�A���Զ����ʼ��ɲ�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
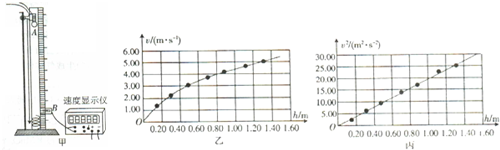
 ��ͼ��ʾ��������ʱ���̶�������̨�ϣ����������ֽ���Ӿ�ֹ��ʼ�������䣬���ô�װ�ÿɲⶨ�������ٶȣ�
��ͼ��ʾ��������ʱ���̶�������̨�ϣ����������ֽ���Ӿ�ֹ��ʼ�������䣬���ô�װ�ÿɲⶨ�������ٶȣ� �鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
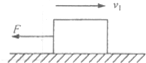 ��ˮƽ������С��龭����ͼ��ʾ��λ��ʱ���ٶȴ�СΪv1������ˮƽ���ң���������С���ʩ��ˮƽ����ĺ���F������һ��ʱ���С����ٴλص�ͼʾλ�ã��ٶȴ�СΪv2������ˮƽ������v2��v1����֪F=kmg����С�����ˮƽ����֮��Ķ�Ħ������Ϊ��������
��ˮƽ������С��龭����ͼ��ʾ��λ��ʱ���ٶȴ�СΪv1������ˮƽ���ң���������С���ʩ��ˮƽ����ĺ���F������һ��ʱ���С����ٴλص�ͼʾλ�ã��ٶȴ�СΪv2������ˮƽ������v2��v1����֪F=kmg����С�����ˮƽ����֮��Ķ�Ħ������Ϊ��������| A�� | $\frac{{v}_{1}^{2}+{v}_{2}^{2}}{k��{v}_{1}^{2}-{v}_{2}^{2}��}$ | B�� | $\frac{k��{v}_{1}^{2}+{v}_{2}^{2}��}{{v}_{1}^{2}-{v}_{2}^{2}}$ | ||
| C�� | $\frac{{v}_{1}^{2}-{v}_{2}^{2}}{k��{v}_{1}^{2}+{v}_{2}^{2}��}$ | D�� | $\frac{k��{v}_{1}^{2}-{v}_{2}^{2}��}{{v}_{1}^{2}+{v}_{2}^{2}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
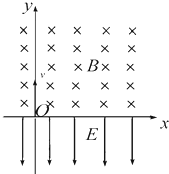 ��ͼ��ʾ����x���Ϸ��д�ֱ��xyƽ���������ǿ�ų����Ÿ�Ӧǿ��ΪB����x���·�����y�Ḻ�������ǿ�糡����ǿΪE��һ����Ϊm������Ϊ-q�����Ӵ�����ԭ��O����y�����������?���֮�����ε���x��ʱ��O�㲻���һ�Σ��������O�ľ���ΪL����
��ͼ��ʾ����x���Ϸ��д�ֱ��xyƽ���������ǿ�ų����Ÿ�Ӧǿ��ΪB����x���·�����y�Ḻ�������ǿ�糡����ǿΪE��һ����Ϊm������Ϊ-q�����Ӵ�����ԭ��O����y�����������?���֮�����ε���x��ʱ��O�㲻���һ�Σ��������O�ľ���ΪL�����鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com