
| A. | 地球绕太阳运行的周期及地球离太阳的距离 | |
| B. | 月球绕地球运行的周期及月球离地球的距离 | |
| C. | 人造地球卫星的质量运行周期 | |
| D. | 若不考虑地球自转,已知地球的半径及重力加速度 |
分析 地球、月球、人造卫星等做匀速圆周运动,它们受到的万有引力充当向心力,用它们的运动周期表示向心力,由万有引力定律结合牛顿第二定律列式求中心天体的质量,然后由选项条件判断正确的答案.
解答 解:A、地球绕太阳运动的周期和地球与太阳的距离,根据万有引力提供向心力:$\frac{GMm}{{r}^{2}}$=$\frac{m•4{π}^{2}r}{{T}^{2}}$ 其中m为地球质量,在等式中消去,只能求出太阳的质量M.也就是说只能求出中心体的质量.故A错误.
B、同理,已知月球绕地球运行的周期T及月球中心到地球中心的距离r,能求出地球的质量,故B正确.
C、人造卫星绕地球做匀速圆周运动,它受到地球的万有引力充当向心力$G\frac{Mm}{{R}^{2}}=m\frac{4{π}^{2}}{{T}^{2}}R$.因此,要计算地球质量,还必须要知道地球的半径,故C错误;
D、地球表面的物体受到的地球的重力等于万有引力,即mg=$\frac{GMm}{{r}^{2}}$,因此,可求出地球的质量M=$\frac{{r}^{2}g}{G}$,故D正确.
故选:BD.
点评 解答万有引力定律在天体运动中的应用时要明确天体做匀速圆周运动,其受到的万有引力提供向心力,会用线速度、角速度、周期表示向心力,同时注意公式间的化简.


科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
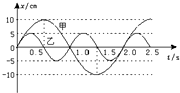
| A. | 两弹簧振子完全相同 | |
| B. | 两弹簧振子所受回复力最大值之比F甲:F乙=2:1 | |
| C. | 振子甲速度为零时,振子乙速度最大 | |
| D. | 振子甲的质量是振子乙的两倍 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
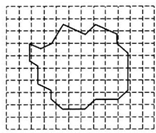 在做”用油膜法估测分子大小”的实验时,油酸酒精溶液的浓度为每1000mL.溶液中有纯油酸1mL,用注射器测得1mL上述溶液有200滴,把一滴该溶液滴入盛水的表面撒有痱子粉的浅盘里,待水面稳定后,测得油酸膜的近似轮廓如图所示,图中正方形小方格的边长为1cm,则每一滴油酸酒精溶液中含有纯油酸的体积是5×10-6mL,油酸膜的面积是40cm2.根据上述数据,估测出油酸分子的直径是1.25nm.(结果均保留两位有效数字)
在做”用油膜法估测分子大小”的实验时,油酸酒精溶液的浓度为每1000mL.溶液中有纯油酸1mL,用注射器测得1mL上述溶液有200滴,把一滴该溶液滴入盛水的表面撒有痱子粉的浅盘里,待水面稳定后,测得油酸膜的近似轮廓如图所示,图中正方形小方格的边长为1cm,则每一滴油酸酒精溶液中含有纯油酸的体积是5×10-6mL,油酸膜的面积是40cm2.根据上述数据,估测出油酸分子的直径是1.25nm.(结果均保留两位有效数字)查看答案和解析>>
科目:高中物理 来源: 题型:解答题
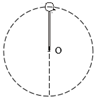 如图所示,质量为m=0.2kg的小球固定在L=0.9m的轻杆的一端,杆可绕O点的水平轴在竖直平面内转动,g=10m/s2,求:
如图所示,质量为m=0.2kg的小球固定在L=0.9m的轻杆的一端,杆可绕O点的水平轴在竖直平面内转动,g=10m/s2,求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
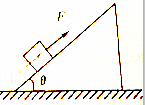 如图所示,力F的功率不变,可使物体沿倾斜角为θ的粗糙斜面乙速度为v匀速上升,若此力拉着该物体沿斜面下滑,可使物体以速度2v匀速下滑,若此力拉着该物体在同样粗糙的水平路面上运动时,则匀速运动的速度为多少?
如图所示,力F的功率不变,可使物体沿倾斜角为θ的粗糙斜面乙速度为v匀速上升,若此力拉着该物体沿斜面下滑,可使物体以速度2v匀速下滑,若此力拉着该物体在同样粗糙的水平路面上运动时,则匀速运动的速度为多少?查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 有一固定轨道ABCD如图所示,AB段为四分之一光滑圆弧轨道,其半径为R,BC段是水平光滑轨道,CD段是光滑斜面轨道,BC和斜面CD间用一小段光滑圆弧连接.有编号为1、2、3、4完全相同的4个小球(小球不能视为质点,其半径r<R),紧挨在一起从圆弧轨道上某处由静止释放,经平面BC到斜面CD上,忽略一切阻力,则下列说法正确的是( )
有一固定轨道ABCD如图所示,AB段为四分之一光滑圆弧轨道,其半径为R,BC段是水平光滑轨道,CD段是光滑斜面轨道,BC和斜面CD间用一小段光滑圆弧连接.有编号为1、2、3、4完全相同的4个小球(小球不能视为质点,其半径r<R),紧挨在一起从圆弧轨道上某处由静止释放,经平面BC到斜面CD上,忽略一切阻力,则下列说法正确的是( )| A. | 四个小球在整个运动过程中始终不分离 | |
| B. | 当四个小球在圆弧轨道上运动时,2号球对3号球不做功 | |
| C. | 当四个小球在圆弧轨道上运动时,2号球对3号球做正功 | |
| D. | 当四个小球在CD斜面轨道上运动时,2号球对3号球做正功 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
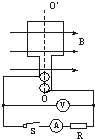 如图所示为交流发电机示意图,匝数为n=100匝的矩形线圈,边长分别为 10cm和20cm,内阻为5Ω,在磁感应强度B=0.5T的匀强磁场中绕OO′轴以50$\sqrt{2}$rad/s的角速度匀速转动,转动开始时线圈平面与磁场方向平行,线圈通过电刷和外部20Ω的电阻R相接.求电键S合上后.
如图所示为交流发电机示意图,匝数为n=100匝的矩形线圈,边长分别为 10cm和20cm,内阻为5Ω,在磁感应强度B=0.5T的匀强磁场中绕OO′轴以50$\sqrt{2}$rad/s的角速度匀速转动,转动开始时线圈平面与磁场方向平行,线圈通过电刷和外部20Ω的电阻R相接.求电键S合上后.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com