
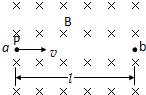
 如图所示,在一竖直平面内有水平匀强磁场,磁感应强度B的方向垂直该竖直平面向里.竖直平面中a、b两点在同一水平线上,两点相距l.带电量 q>0,质量为m的小球P,以初速度v从a对准b射入磁场.略去空气阻力,不考虑P与地面接触的可能性,设定q、m 和B均为不变的给定量.
如图所示,在一竖直平面内有水平匀强磁场,磁感应强度B的方向垂直该竖直平面向里.竖直平面中a、b两点在同一水平线上,两点相距l.带电量 q>0,质量为m的小球P,以初速度v从a对准b射入磁场.略去空气阻力,不考虑P与地面接触的可能性,设定q、m 和B均为不变的给定量. 分析 (1)小球受重力和洛仑兹力,根据平衡条件列式求解;
(2)(3)设第一问的速度为v1,将速度v分解为v1和另一个速度v2,则以v1向右做匀速直线运动的同时,以速度v2做匀速圆周运动,实际运动是两个分运动的合运动;故通过b点时,圆周运动是整数圈数;
(4)初速度为零,分解为一对相反的水平速度,大小等于第一问的速度值即可.
解答 解:(1)小球受重力和洛仑兹力,做直线运动,合力如果不为零,与速度不共线,矛盾,故小球做匀速直线运动,故:
mg=qvB
解得:
v=$\frac{mg}{qB}$
(2)如果速度不等于$\frac{mg}{qB}$,则洛仑兹力不等于重力,做曲线运动;
将速度v分解为向右的速度v1=$\frac{mg}{qB}$和水平速度v2=|v-$\frac{mg}{qB}$|,故小球的实际运动是以v1向右做匀速直线运动和以速度v2做匀速圆周运动的合运动;
运动时间为:t=$\frac{l}{{v}_{1}}=\frac{lqB}{mg}$;
粒子的圆周运动的周期:T=$\frac{2πm}{qB}$,故:
t=nT
联立解得:
l=$\frac{{2πn{m^2}g}}{{{q^2}{B^2}}}$ (其中n=1、2、3、…)
(3)由第二问分析可知:t=nT=$\frac{2πnm}{qB}$ (其中n=1、2、3、…)
(4)初速度为零,分解为一对相反的水平速度,分速度大小均为$\frac{mg}{qB}$;
故水平分运动的位移为l的运动时间为:t=$\frac{l}{{v}_{1}}$=$\frac{2πn•m}{qB}$(其中n=1、2、3、…)
小球的圆周运动(分运动)的周期:T=$\frac{2πm}{qB}$,
故t=nT
故小球也可以通过b点;
当两个分运动的速度相同时,速度最大,故:
vmax=2v1=$\frac{2mg}{qB}$
答:(1)若无论 l 取什么值,均可使P 经直线运动通过b 点,问v应为$\frac{mg}{qB}$;
(2)若v为(1)问可取值之外的任意值,则当l=$\frac{{2πn{m^2}g}}{{{q^2}{B^2}}}$ (其中n=1、2、3、…)时,可使P必定会经曲线运动通过b点;
(3)对每一个满足(2)问要求的l值,各种可能的曲线运动对应的P从a到b所经过的时间均为$\frac{2πnm}{qB}$ (其中n=1、2、3、…).
(4)对每一个满足(2)问要求的l值,P能从a静止释放后通过b点,P在以后运动过程中可达到的最大运动速率vmax为$\frac{2mg}{qB}$.
点评 本题思路冷僻,关键是将合运动分解为一个匀速直线运动和一个匀速圆周运动进行分析,故只要能够到达b点,时间都是相等的,不难.


科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
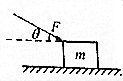 如图所示,质量为m的物体放在水平地面上,物体与地面间的动摩擦因数为μ,推力方向与水平面的夹角为θ,推力多大时可使物体沿水平地面匀速滑动?
如图所示,质量为m的物体放在水平地面上,物体与地面间的动摩擦因数为μ,推力方向与水平面的夹角为θ,推力多大时可使物体沿水平地面匀速滑动?查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
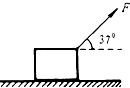 一质量为2kg的物体放在水平面上,处于静止状态.物体与水平面之间的动摩擦因数为0.1在一与水平方向成37°角的斜向上的10N的恒力作用下开始运动,10秒后撤去水平恒力,求20s内的位移和20s末的速度.
一质量为2kg的物体放在水平面上,处于静止状态.物体与水平面之间的动摩擦因数为0.1在一与水平方向成37°角的斜向上的10N的恒力作用下开始运动,10秒后撤去水平恒力,求20s内的位移和20s末的速度.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 伽利略通过实验和逻辑推理说明力是维持物体运动的原因 | |
| B. | 只有在国际单位制中,牛顿第二定律的表达式才是F=ma | |
| C. | 伽利略认为自由落体运动是速度随位移均匀变化的运动 | |
| D. | 在物理问题的研究中,如果不需要考虑物体本身的大小和形状时,用质点来代替物体的方法叫假设法 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题

| A. | 小滑块A和长木板B相对运动时的加速度aA=4.0m/s2,方向水平向左,aB=1.0m/s2,方向水平向右 | |
| B. | 小滑块A在相对地面的速度为零时,长木板B的速度 vB=1.5m/s | |
| C. | 小滑块A相对地面的速度为零时,长木板B相对地面运动已发生的位移 x=0.875m | |
| D. | 长木板B的长度 l=1.6m |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
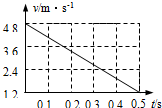 一质量m=1.0kg的滑块以一定的初速度冲上一倾角为37°足够长的斜面,某同学利用传感器测出了滑块冲上斜面过程中多个时刻的瞬时速度,如图所示为通过计算机绘制出的滑块上滑过程的v-t图.已知sin37°=0.6,cos37°=0.8,g取10m/s2.求:
一质量m=1.0kg的滑块以一定的初速度冲上一倾角为37°足够长的斜面,某同学利用传感器测出了滑块冲上斜面过程中多个时刻的瞬时速度,如图所示为通过计算机绘制出的滑块上滑过程的v-t图.已知sin37°=0.6,cos37°=0.8,g取10m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,A、B 两物块的质量分别为 2m 和 m,静止叠放在水平地面上.A、B 间的动摩擦因数为μ,B 与地面间的动摩擦因数为$\frac{1}{2}$μ.最大静摩擦力等于滑动摩擦力,重力加速度为 g.现对 A 施加一水平拉力 F,则( )
如图所示,A、B 两物块的质量分别为 2m 和 m,静止叠放在水平地面上.A、B 间的动摩擦因数为μ,B 与地面间的动摩擦因数为$\frac{1}{2}$μ.最大静摩擦力等于滑动摩擦力,重力加速度为 g.现对 A 施加一水平拉力 F,则( )| A. | 当 F<2 μmg 时,A、B 都相对地面静止 | |
| B. | 当 F=$\frac{5}{2}$μmg 时,A 的加速度为$\frac{1}{3}$μg | |
| C. | 当 F>3 μmg 时,A 相对 B 滑动 | |
| D. | 无论 F 为何值,B 的加速度不会超过$\frac{1}{2}$μg |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com