
| A. | 两星质量一定相等 | |
| B. | 两星质量之和为m1+m2=$\frac{4{π}^{2}({R}_{1}+{R}_{2})^{3}}{G{T}^{2}}$ | |
| C. | 两星质量之比为$\frac{{m}_{1}}{{m}_{2}}$=$\frac{{R}_{1}}{{R}_{2}}$ | |
| D. | 有一颗星质量必为$\frac{4{π}^{2}{R}_{1}({R}_{1}+{R}_{2})^{2}}{G{T}^{2}}$ |
分析 双星系统中,两颗星球绕同一点做匀速圆周运动,且两者始终与圆心共线,相同时间内转过相同的角度,即角速度相等,则周期也相等.但两者做匀速圆周运动的半径不相等.
解答 解:A、双星的周期相等,则角速度相等,两星质量分别为m1和m2,都绕连线上O点作周期为T的圆周运动,星球1和星球2到O的距离分别为R1和R2.
由万有引力定律提供向心力:
对m1:$G\frac{{m}_{1}{m}_{2}}{{L}^{2}}={m}_{1}{(\frac{2π}{T})}^{2}{R}_{1}$
对于m1而言,所受万有引力大小恒定,其圆周运动向心力与万有引力相等,根据表达式知,其质量与转动半径成反比.
得:${m}_{2}=\frac{4{π}^{2}{L}^{2}{R}_{1}}{G{T}^{2}}$ ①
对m2:$G\frac{{m}_{1}{m}_{2}}{{L}^{2}}={m}_{2}{(\frac{2π}{T})}^{2}{R}_{2}$
${m}_{1}=\frac{4{π}^{2}{L}^{2}{R}_{2}}{G{T}^{2}}$ ②
比较①②可知,两星质量不一定相等.故A错误;
B、由几何关系知:R1+R2=L ③
三式联立解得:m总=m1+m2=$\frac{4{π}^{2}{L}^{2}}{G{T}^{2}}({R}_{1}+{R}_{2})=\frac{4{π}^{2}({R}_{1}+{R}_{2})^{3}}{G{T}^{2}}$故B正确;
C、联立①②可得:$\frac{{m}_{1}}{{m}_{2}}=\frac{{R}_{2}}{{R}_{1}}$.故C错误;
D、联立①③可得:${m}_{2}=\frac{4{π}^{2}({R}_{1}+{R}_{2})^{2}{R}_{1}}{G{T}^{2}}$.故D正确.
故选:BD
点评 处理双星问题必须注意两点:
(1)两颗星球运行的角速度、周期相等;
(2)轨道半径不等于引力距离.弄清每个表达式中各字母的含义,在示意图中相应位置标出相关量,可以最大限度减少错误.


科目:高中物理 来源: 题型:多选题
| A. | 保持质量不变,将它们间的距离增大到2R | |
| B. | 保持质量不变,将它们间的距离减小到原来的R/2 | |
| C. | 保持距离不变,将它们的质量都变为原来的2倍 | |
| D. | 将它们的质量及距离都变为原来的2倍 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题

| A. | 探测器的速度一直减小 | |
| B. | 探测器在距星球A为$\frac{L}{4}$处加速度为零 | |
| C. | 若探测器能到达星球B,其速度可能恰好为零 | |
| D. | 若探测器能到达星球B,其所受的合力先变小后变大 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 物体初动量方向一定与这个冲量的方向相反 | |
| B. | 物体末动量一定是负值 | |
| C. | 物体动量的增量一定与规定的正方向相反 | |
| D. | 物体的动量一定减小 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 16F | B. | 8F | C. | 4F | D. | 2F |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
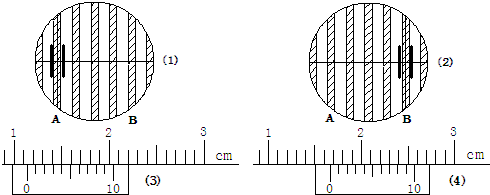
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
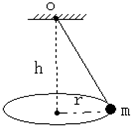 如图所示,在“用圆锥摆验证向心力表达式”的实验中,若测得小球质量为m,圆半径为r,小球到悬点大竖直高度为h,则小球所受向心力大小为$\frac{mgr}{h}$.
如图所示,在“用圆锥摆验证向心力表达式”的实验中,若测得小球质量为m,圆半径为r,小球到悬点大竖直高度为h,则小球所受向心力大小为$\frac{mgr}{h}$.查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com