

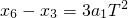 ①
①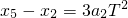 ②
②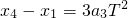 ③
③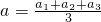 =
=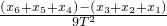 =0.63m/s2
=0.63m/s2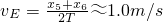


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中物理 来源: 题型:

查看答案和解析>>
科目:高中物理 来源: 题型:阅读理解
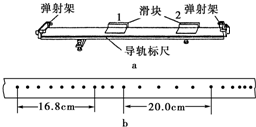 (2009?肇庆一模)某同学利用打点计时器和气垫导轨做验证动量守恒定律的实验.气垫导轨装置如图a所示,所用的气垫导轨装置由导轨、滑块、弹射架等组成.在空腔导轨的两个工作面上均匀分布着一定数量的小孔,向导轨空腔内不断通入压缩空气,空气会从小孔中喷出,使滑块稳定地漂浮在导轨上,这样就大大减小了因滑块和导轨之间的摩擦而引起的误差.
(2009?肇庆一模)某同学利用打点计时器和气垫导轨做验证动量守恒定律的实验.气垫导轨装置如图a所示,所用的气垫导轨装置由导轨、滑块、弹射架等组成.在空腔导轨的两个工作面上均匀分布着一定数量的小孔,向导轨空腔内不断通入压缩空气,空气会从小孔中喷出,使滑块稳定地漂浮在导轨上,这样就大大减小了因滑块和导轨之间的摩擦而引起的误差.查看答案和解析>>
科目:高中物理 来源: 题型:
查看答案和解析>>
科目:高中物理 来源: 题型:

查看答案和解析>>
科目:高中物理 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com