
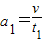 =
=

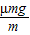 =1.25m/s2,
=1.25m/s2,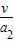 =8s
=8s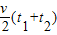 =
=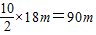


科目:高中物理 来源: 题型:
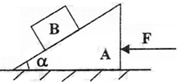 如图,在水平面上有一质量为M的楔形木块A,其倾角为α,一质量为m的木块放在A的斜面上,现对A施一水平推力F,恰使B与A不发生相对滑动,忽略一切摩擦,则B对A的压力大小为( )
如图,在水平面上有一质量为M的楔形木块A,其倾角为α,一质量为m的木块放在A的斜面上,现对A施一水平推力F,恰使B与A不发生相对滑动,忽略一切摩擦,则B对A的压力大小为( )查看答案和解析>>
科目:高中物理 来源: 题型:
查看答案和解析>>
科目:高中物理 来源: 题型:
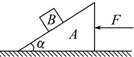 (2003?肇庆模拟)如图所示,在水平面上有一质量为M的楔形木块A,其倾斜角为α,一质量为m的木块B放在A的斜面上.现对A施一水平推力F,使B与A不发生相对滑动,忽略一切摩擦,则B对A的压力大小为( )
(2003?肇庆模拟)如图所示,在水平面上有一质量为M的楔形木块A,其倾斜角为α,一质量为m的木块B放在A的斜面上.现对A施一水平推力F,使B与A不发生相对滑动,忽略一切摩擦,则B对A的压力大小为( )查看答案和解析>>
科目:高中物理 来源: 题型:
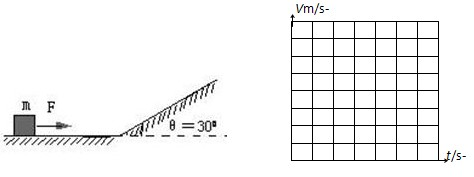 如图所示,在水平面上有一质量为m的物体,在水平拉力作用下由静止开始运动一段距离后到达一斜面底端,这时撤去外力物体冲上斜面,上滑的最大距离和在平面 上移动的距离相等,然后物体又沿斜面下滑,恰好停在平面上的出发点.已知斜面倾角θ=300,斜面与平面上的动摩擦因数相同.
如图所示,在水平面上有一质量为m的物体,在水平拉力作用下由静止开始运动一段距离后到达一斜面底端,这时撤去外力物体冲上斜面,上滑的最大距离和在平面 上移动的距离相等,然后物体又沿斜面下滑,恰好停在平面上的出发点.已知斜面倾角θ=300,斜面与平面上的动摩擦因数相同.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com