
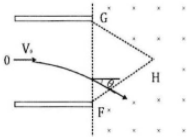
 ƽ�а������ֱ���µ���ǿ�糡���ӵ糡��߽���е�O��ˮƽ��������һ����������ӣ�������������������ٶ�Ϊv0�����糡ƫת������ˮƽ�����30��Ǵӵ糡�б߽���P������糡�����ɵȱ�������GFHΧ�ɵ�������Ȼ���ٽ�����ͼ��ʾ����ǿ�ų����ų�����ֱ������������ڴų����˶��պþ���H�㣮��֪ƽ�а�ij���Ϊl=$\frac{\sqrt{3}}{2}$d���ȱ�����������߳�������Ϊd�����ӵ�����Ϊm�������Ϊq��
ƽ�а������ֱ���µ���ǿ�糡���ӵ糡��߽���е�O��ˮƽ��������һ����������ӣ�������������������ٶ�Ϊv0�����糡ƫת������ˮƽ�����30��Ǵӵ糡�б߽���P������糡�����ɵȱ�������GFHΧ�ɵ�������Ȼ���ٽ�����ͼ��ʾ����ǿ�ų����ų�����ֱ������������ڴų����˶��պþ���H�㣮��֪ƽ�а�ij���Ϊl=$\frac{\sqrt{3}}{2}$d���ȱ�����������߳�������Ϊd�����ӵ�����Ϊm�������Ϊq������ ��1������ƽ���˶����ɸ���ĩ�ٶȵķ������ƫ���������ٶȣ������õ���ǿ��С��
��2���������ӽ���ų�ʱ���ٶȷ��������ڴų��е����㣬�ɼ��ι�ϵ����˶��뾶���ٸ���������������������⼴�ɣ�
��3���ֱ������ƽ���˶����ɼ�����ֱ���˶�������ý���ų�ǰ���뿪�ų�����˶�ʱ�䣻�ڴų��е��˶�ʱ����ݼ��ι�ϵ������Ľǣ��������ڹ�ʽ��⼴�ɣ�
��� 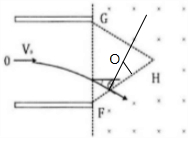 �⣺��1�����������ڵ糡���˶�ֻ�ܵ糡�����ã����ԣ���������ƽ���˶������ٶ�Ϊ��$a=\frac{qE}{m}$��
�⣺��1�����������ڵ糡���˶�ֻ�ܵ糡�����ã����ԣ���������ƽ���˶������ٶ�Ϊ��$a=\frac{qE}{m}$��
��ô����ƽ���˶����ٶȡ�λ�ƹ�ʽ�ɵã�$l=\frac{\sqrt{3}}{2}d={v}_{0}t$��$y=\frac{1}{2}a{t}^{2}$��$tan��=\frac{{v}_{y}}{{v}_{x}}=\frac{at}{{v}_{0}}$��
������$E=\frac{ma}{q}=\frac{m{v}_{0}tan��}{qt}=\frac{m{{v}_{0}}^{2}tan��}{\frac{\sqrt{3}}{2}qd}=\frac{2m{{v}_{0}}^{2}}{3qd}$
$y=\frac{1}{2}a{t}^{2}=\frac{d}{4}$��
��2���ɼ��ι�ϵ�ɵ������ڴų�����Բ���˶��İ뾶Ϊ��
$R=\frac{d-��\frac{1}{2}d-y��}{2cos30��}=\frac{\sqrt{3}}{4}d$
�����ڴų����˶�������Ϊ��$v=\frac{{v}_{0}}{cos30��}=\frac{2\sqrt{3}}{3}{v}_{0}$
���ԣ������������ṩ�������ɵã�$Bvq=\frac{m{v}^{2}}{R}$��
��ã�$B=\frac{mv}{qR}=\frac{8m{v}_{0}}{3qd}$��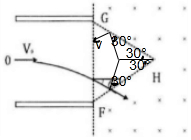 ��3�����Ӵ�O��P���˶�ʱ��Ϊ��${t}_{1}=\frac{l}{{v}_{0}}=\frac{\sqrt{3}d}{2{v}_{0}}$��
��3�����Ӵ�O��P���˶�ʱ��Ϊ��${t}_{1}=\frac{l}{{v}_{0}}=\frac{\sqrt{3}d}{2{v}_{0}}$��
���Ӵ�P�㵽����ų����˶�ʱ��Ϊ��${t}_{2}=\frac{\frac{1}{2}d-y}{v}=\frac{\sqrt{3}d}{8{v}_{0}}$��
�����ڴų����˶���ת�������Ľ�Ϊ240�㣬���ӵ��˶�����Ϊ��
$T=\frac{2��R}{v}=\frac{2��m}{qB}=\frac{3��d}{4{v}_{0}}$��
���ԣ������ڴų����˶���ʱ��Ϊ��
${t}_{3}=\frac{2}{3}T$=$\frac{��d}{2{v}_{0}}$��
�����ɴų�����ֱ��O��Ĺ������O�㵽����ų��Ĺ�����ȫ�Գƣ����ԣ��ù����õ�ʱ��Ϊ��
${t}_{4}={t}_{1}+{t}_{2}=\frac{5\sqrt{3}d}{8{v}_{0}}$��
���ԣ����Ӵӿ�ʼ����糡���ٴη��ص�O������ʱ��Ϊ��
$t={t}_{1}+{t}_{2}+{t}_{3}+{t}_{4}=��\frac{5\sqrt{3}}{4}+\frac{��}{2}��\frac{d}{{v}_{0}}$��
�𣺣�1����ǿ�糡�ij�ǿ��СEΪ$\frac{2m{{v}_{0}}^{2}}{3qd}$�������ڵ糡�е�ƫ����yΪ$\frac{d}{4}$��
��2����ǿ�ų��ĴŸ�Ӧǿ�ȴ�СBΪ$\frac{8m{v}_{0}}{3qd}$��
��2�������ٴη���ƽ�а������ʱ���������糡��Ϊ����С���䣩���ӽ��᷵�س���O�㣬�����Ӵӿ�ʼ����糡���ٴη��ص�O������ʱ��Ϊ$��\frac{5\sqrt{3}}{4}+\frac{��}{2}��\frac{d}{{v}_{0}}$��
���� ���������ڴų����˶����⣬һ����������������������ð뾶�ı���ʽ��Ȼ����ݼ��ι�ϵ��ð뾶������������⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�������
 ��ͼ��ʾ��ԲͲ���ڱڹ⻬��һ��B�̶�����ֱת��OO���ϣ�ԲͲ������ת��������ˮƽ��ļн�ʼ��Ϊ30�㣬��Ͳ����һ�������ʵ������ӵ�С��A��С��ֱ����С��ԲͲ�ھ�����A������Ϊm�����ɵ���һ�˹̶���ԲͲ��B�ˣ�����ԭ��Ϊ$\frac{3}{2}$L����ԲͲ��ֹʱA��B֮��ľ���ΪL��LԶ����С��ֱ����������ԲͲ��ʼת��������ٶȴ�0��ʼ�����������ٶ�����ijһֵʱ��������ת������ʱС��A��B֮��ľ���Ϊ2L���������ٶȴ�СΪg����ԲͲ��������ת��ʱ�Ľ��ٶȦ�0��
��ͼ��ʾ��ԲͲ���ڱڹ⻬��һ��B�̶�����ֱת��OO���ϣ�ԲͲ������ת��������ˮƽ��ļн�ʼ��Ϊ30�㣬��Ͳ����һ�������ʵ������ӵ�С��A��С��ֱ����С��ԲͲ�ھ�����A������Ϊm�����ɵ���һ�˹̶���ԲͲ��B�ˣ�����ԭ��Ϊ$\frac{3}{2}$L����ԲͲ��ֹʱA��B֮��ľ���ΪL��LԶ����С��ֱ����������ԲͲ��ʼת��������ٶȴ�0��ʼ�����������ٶ�����ijһֵʱ��������ת������ʱС��A��B֮��ľ���Ϊ2L���������ٶȴ�СΪg����ԲͲ��������ת��ʱ�Ľ��ٶȦ�0���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | 9N•s | B�� | 10N•s | C�� | 11N•s | D�� | 12N•s |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ���ڹ⻬�ġ�V����©���У���������ˮƽ��������Բ���˶�����ʱС���ܵ������У�������
��ͼ��ʾ���ڹ⻬�ġ�V����©���У���������ˮƽ��������Բ���˶�����ʱС���ܵ������У�������| A�� | ���� | B�� | ������֧���� | ||
| C�� | ������������ | D�� | ������֧������������ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��

| A�� | ��ͼa������ͨ�����ŵ���ߵ㴦��ʧ��״̬ | |
| B�� | ��ͼb����һԲ�ڣ�����ȣ�������Բ�ĸ߲��䣬��Բ�ڵĽ��ٶȲ��� | |
| C�� | ��ͼc��ͬһС���ڹ⻬���̶���ԲͲ�ڵ�A��Bλ���Ⱥ�ֱ�������Բ���˶�������A��B��λ��С��Ľ��ٶȼ�����Ͳ�ڵ�֧������С��� | |
| D�� | ��ͼd����ת�䳬���涨�ٶ���ʻʱ���ڹ������Ե���м�ѹ���� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
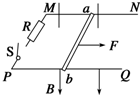 ��ͼ��ʾ����ˮƽƽ�з��õ������⻬�ij�ֱ������MN��PQ�ϣ�����һ��ֱ�����ab��ab�뵼�촹ֱ�����ڵ����ij���Ϊ20cm���ⲿ�ֵĵ���r=0.02�����������ڵĿռ�����ֱ���µ���ǿ�ų����Ÿ�Ӧǿ��B=0.20T������R=0.08�����������費�ƣ�ab������Ϊ0.02kg��
��ͼ��ʾ����ˮƽƽ�з��õ������⻬�ij�ֱ������MN��PQ�ϣ�����һ��ֱ�����ab��ab�뵼�촹ֱ�����ڵ����ij���Ϊ20cm���ⲿ�ֵĵ���r=0.02�����������ڵĿռ�����ֱ���µ���ǿ�ų����Ÿ�Ӧǿ��B=0.20T������R=0.08�����������費�ƣ�ab������Ϊ0.02kg���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
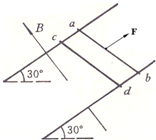 ��ͼʾ��ƽ�����㹻���������⻬�������죬���1.0m����ˮƽ��н�Ϊ30�㣬���Ƶ��裬��������ǿ�ų���ֱ��������ƽ�棬�Ÿ�Ӧǿ��B=0.4T����ֱ���������������ab��cd�����Ⱦ�Ϊ1.0m�������Ϊ0.1���������ֱ�Ϊ0.1kg��0.4kg�������������������Ӵ������ҿ��ص������ɻ�������ab�������������£��Ժ㶨�ٶ�v=2m/s���ŵ������ϻ�����cd�����ɾ�ֹ�ͷţ�����
��ͼʾ��ƽ�����㹻���������⻬�������죬���1.0m����ˮƽ��н�Ϊ30�㣬���Ƶ��裬��������ǿ�ų���ֱ��������ƽ�棬�Ÿ�Ӧǿ��B=0.4T����ֱ���������������ab��cd�����Ⱦ�Ϊ1.0m�������Ϊ0.1���������ֱ�Ϊ0.1kg��0.4kg�������������������Ӵ������ҿ��ص������ɻ�������ab�������������£��Ժ㶨�ٶ�v=2m/s���ŵ������ϻ�����cd�����ɾ�ֹ�ͷţ������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
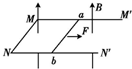 ��ͼ��ʾ�����費�����㹻����U�ν�����ܷ����ھ�Եˮƽ���ϣ������ˮƽ���Ķ�Ħ������Ϊ�̣���ܵĿ���ΪL������Ϊm1������Ϊm2������ΪR�ľ��ȵ����ab��ֱ���ڿ���ϣ�����װ�ô�����ֱ���ϵ���ǿ�ų��У��Ÿ�Ӧǿ�ȴ�СΪB���ֶԵ����ʩ��һˮƽ����F��ʹ���Ӿ�ֹ��ʼ��Ħ�����˶����������˶��ٶȴﵽijֵʱ��ܿ�ʼ�˶��������ܽӴ����ã������ˮƽ�������Ħ�����뻬��Ħ������ȣ��������ٶ�Ϊg��
��ͼ��ʾ�����費�����㹻����U�ν�����ܷ����ھ�Եˮƽ���ϣ������ˮƽ���Ķ�Ħ������Ϊ�̣���ܵĿ���ΪL������Ϊm1������Ϊm2������ΪR�ľ��ȵ����ab��ֱ���ڿ���ϣ�����װ�ô�����ֱ���ϵ���ǿ�ų��У��Ÿ�Ӧǿ�ȴ�СΪB���ֶԵ����ʩ��һˮƽ����F��ʹ���Ӿ�ֹ��ʼ��Ħ�����˶����������˶��ٶȴﵽijֵʱ��ܿ�ʼ�˶��������ܽӴ����ã������ˮƽ�������Ħ�����뻬��Ħ������ȣ��������ٶ�Ϊg���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �䵽������� | B�� | ��ֹ�ڵ����Ͽ�ij�㲻�� | ||
| C�� | �����������߷���ɳ� | D�� | ���¡������߷���ɳ� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com