
分析 由万有引力提供向心力,求出所给量的表达式,据表达式求比值.
解答 解:(1)由万有引力提供向心力得:T=$2π\sqrt{\frac{{r}^{3}}{GM}}$,则$\frac{{T}_{甲}}{{T}_{乙}}=\sqrt{\frac{{r}_{甲}^{3}}{{r}_{乙}^{3}}}$=$\sqrt{\frac{{2}^{3}}{{3}^{3}}}$=2$\sqrt{2}$:3$\sqrt{3}$
(2)由万有引力提供向心力得:a=$\frac{GM}{{r}^{2}}$,则$\frac{{a}_{甲}}{{a}_{乙}}=\frac{{r}_{乙}^{2}}{{r}_{甲}^{2}}$=$\frac{9}{4}$
(3)万有引力:F=$G\frac{Mm}{{r}^{2}}$,则:$\frac{{F}_{甲}}{{F}_{乙}}=\frac{{m}_{甲}}{{m}_{乙}}×\frac{{r}_{乙}^{2}}{{r}_{甲}^{2}}$=$\frac{3}{4}$
故答案为:(1)2$\sqrt{2}$:3$\sqrt{3}$ (2)9:4 (3)3:4
点评 明确万有引力提供向心力,确定出各量的表达式是解题的关键.不难.


 名校课堂系列答案
名校课堂系列答案科目:高中物理 来源: 题型:多选题
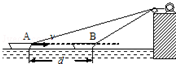 如图,用跨过光滑定滑轮的缆绳将海面上一艘小船直线拖向岸边.已知拖动缆绳的电动机功率恒为P,小船的质量为m,小船所受到水的阻力大小恒为f,经过A点时的速度大小为v,小船从A点沿直线运动到B点经历时间为t,此时缆绳与水平面夹角为θ,A、B两点间水平距离为d,缆绳质量忽略不计.则( )
如图,用跨过光滑定滑轮的缆绳将海面上一艘小船直线拖向岸边.已知拖动缆绳的电动机功率恒为P,小船的质量为m,小船所受到水的阻力大小恒为f,经过A点时的速度大小为v,小船从A点沿直线运动到B点经历时间为t,此时缆绳与水平面夹角为θ,A、B两点间水平距离为d,缆绳质量忽略不计.则( )| A. | 小船经过B点时的速度大小为VB=$\sqrt{{v}^{2}+\frac{2(Pt-fd)}{m}}$ | |
| B. | 小船经过B点时绳子对小船的拉力大小为$\frac{Pcosθ}{\sqrt{{v}^{2}+\frac{2(Pt-fd)}{m}}}$ | |
| C. | 小船经过A点时电动机牵引绳子的速度大小为$\frac{v}{cosθ}$ | |
| D. | 小船经过B点时的加速度大小为$\frac{P}{\sqrt{{m}^{2}{v}^{2}+2m(Pt-fd)}}$-$\frac{f}{m}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
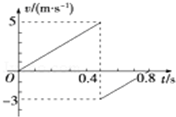 质量为1kg的小球从空中自由下落,与水平地面第一次相碰后反弹到空中某一高度,其速度随时间变化的关系如图所示.若g=10m/s2,则( )
质量为1kg的小球从空中自由下落,与水平地面第一次相碰后反弹到空中某一高度,其速度随时间变化的关系如图所示.若g=10m/s2,则( )| A. | 小球第一次反弹后离开地面的速度的大小为5m/s | |
| B. | 碰撞前后动量改变量的大小为8kg•m/s | |
| C. | 小球是从1.25m高处自由下落的 | |
| D. | 小球反弹起的最大高度为0.45 m |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | $\frac{2πv{G}_{0}{R}^{2}}{GmT}$ | B. | $\frac{v{G}_{0}{R}^{2}}{GmT}$ | C. | $\frac{2v{G}_{0}{R}^{2}}{GmT}$ | D. | $\frac{vG{R}^{2}}{{G}_{0}mT}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
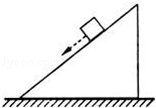 如图所示,质量为M的斜面体放在水平面上,斜面上放一质量为m的物块,当给物块一沿斜面向下的初速度v0时,物块可在斜面上匀速下滑;若在给物块沿斜面向下初速度v0的同时,在物块上施加一平行于斜面向下的拉力,物块可沿斜面加速运动.已知两种情况下斜面体都处于静止状态,则后一种情况和前一种情况相比( )
如图所示,质量为M的斜面体放在水平面上,斜面上放一质量为m的物块,当给物块一沿斜面向下的初速度v0时,物块可在斜面上匀速下滑;若在给物块沿斜面向下初速度v0的同时,在物块上施加一平行于斜面向下的拉力,物块可沿斜面加速运动.已知两种情况下斜面体都处于静止状态,则后一种情况和前一种情况相比( )| A. | 物块对斜面体的压力变大 | B. | 斜面体受地面的摩擦力不变 | ||
| C. | 斜面体对地面的压力变大 | D. | 斜面体受地面的摩擦力变小 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 等于在平衡位置时振子的动能 | |
| B. | 等于在最大位移时弹簧的弹性势能 | |
| C. | 等于任意时刻振子动能与弹簧弹性势能之和 | |
| D. | 位移越大振动能量也越大 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com