
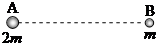 相距为d、质量分别为2m和m的两颗恒星A和B组成双星系统,在万有引力作用下各自绕它们连线上的某一固定点,在同一平面内做匀速圆周运动.设两颗恒星的转动半径分别为RA、RB,速度大小分别为vA、vB,动能分别为EkA、EkB,引力常量为G,则下列关系中正确的是( )
相距为d、质量分别为2m和m的两颗恒星A和B组成双星系统,在万有引力作用下各自绕它们连线上的某一固定点,在同一平面内做匀速圆周运动.设两颗恒星的转动半径分别为RA、RB,速度大小分别为vA、vB,动能分别为EkA、EkB,引力常量为G,则下列关系中正确的是( )| A. | RA=2RB | B. | vA=2vB | C. | EkA=EkB | D. | EkA+EkB=$\frac{G{m}^{2}}{d}$ |
分析 双星靠相互间的万有引力提供向心力,具有相同的角速度,根据万有引力等于向心力列式分析即可.
解答 解:A、对A、B星,都是万有引力提供向心力,故:
$G\frac{2m•m}{d^2}=2m•{ω^2}{R_A}$
$G\frac{2m•m}{d^2}=m•{ω^2}{R_B}$
其中:d=RA+RB
联立解得:
RA=$\frac{1}{3}d$
RB=$\frac{2}{3}d$
$ω=\sqrt{\frac{3Gm}{d^3}}$
故RA=$\frac{1}{2}$RB,故A错误;
B、角速度相等,故:$\frac{v_A}{v_B}=\frac{{{R_A}ω}}{{{R_B}ω}}=\frac{1}{2}$,故B错误;
C、根据${E}_{k}=\frac{1}{2}m{v}^{2}$,有:$\frac{{{E_{kA}}}}{{{E_{kB}}}}=\frac{{\frac{1}{2}(2m){v_A}^2}}{{\frac{1}{2}m{v_B}^2}}=2{(\frac{{{v_A}^{\;}}}{{{v_B}^{\;}}})^2}=2×{(\frac{1}{2})^2}=\frac{1}{2}$,故C错误;
D、由A的分析,有:$ω=\sqrt{\frac{3Gm}{d^3}}$;故${E_{kA}}+{E_{kB}}=\frac{1}{2}(2m){(ω\frac{d}{3})^2}+\frac{1}{2}m{(ω\frac{2d}{3})^2}=\frac{{G{m^2}}}{d}$,故D正确;
故选:D
点评 解决本题的关键知道双星靠相互间的万有引力提供向心力,具有相同的角速度.以及会用万有引力提供向心力进行求解.


科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 8m/s | B. | 12m/s | C. | 10m/s | D. | 14m/s |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
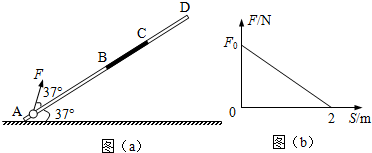 如图(a)所示,固定直杆AD与水平地面成37°角,长度分别为2m和1m的AB段和CD段光滑,长为1m的BC段粗糙.质量为1kg的小球套在直杆上,在方向与直杆成37°角的力F作用下,从杆底端A点处由静止开始运动,小球恰能到达顶端D点.已知力F与小球位移的大小关系如图(b)所示,球与BC段间的动摩擦因数为0.1,sin37°=0.6,cos37°=0.8,取g=10m/s2.求:
如图(a)所示,固定直杆AD与水平地面成37°角,长度分别为2m和1m的AB段和CD段光滑,长为1m的BC段粗糙.质量为1kg的小球套在直杆上,在方向与直杆成37°角的力F作用下,从杆底端A点处由静止开始运动,小球恰能到达顶端D点.已知力F与小球位移的大小关系如图(b)所示,球与BC段间的动摩擦因数为0.1,sin37°=0.6,cos37°=0.8,取g=10m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com