
| A�� | ���Ǽ����������֮������������������ʹ�ù�ʽF=$\frac{K{Q}_{1}{Q}_{2}}{{r}^{2}}$���� | |
| B�� | ��������С��ʹ���ܽ���Ҳ���ÿ��ض��� | |
| C�� | ����õ��������ɣ��������ǵĵ����Ƿ���ͬ������֮��Ŀ�������Сһ����� | |
| D�� | �������ɵĵ�������Ϊԭ����һ�룬����֮��ľ��뱣�ֲ��䣬������֮��Ŀ�������Ϊԭ����һ�� |
���� ������ض��ɵ������������˽������һ�����뻯��ģ�ͣ�
�����������ľ�����������ʱ���������Ѿ����ܿ��ɵ����أ�
����ţ�ٵ������ɽ��B�ܵ��ľ�������A�ܵ��ľ�������ϵ��
��� �⣻AB�����ض��ɵ����������ǣ���պ;�ֹ���ɣ�
������о��������У����������״����С�Լ���ɷֲ����Ժ��Բ��ƣ����ɽ���������һ�����ε㣬�������Ĵ�������ǵ��ɣ�һ��ʵ�ʵĴ������ܷ������ɣ������ʹ����屾���йأ���ȡ������������ʺ;��ȵ�Ҫ��AB����
C������õ���������֮��Ŀ�����Ϊ�������ͷ��������Ĺ�ϵ����Сʼ����ȣ���������Ƿ���ͬ�أ���C��ȷ��
D�����ݿ��ض��ɵļ��㹫ʽF=k$\frac{Qq}{{r}^{2}}$�����������ɵĵ��������Ϊԭ����һ�룬����֮��ľ��뱣�ֲ��䣬������֮��Ŀ�������Ϊԭ����$\frac{1}{4}$����D����
��ѡ��C��
���� ����鱾��һЩ�����Ͷ��ɵ�����������֪���ڴ���������������ʱ���������ձ�����Ļ�������һЩ���ɻ�ȱ������ģ�ͣ�ʹ�����������㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ������
 Ϊ�˽�ȷ�ز���ij����Ԫ���ĵ��裬ijʵ��С�������˲�����
Ϊ�˽�ȷ�ز���ij����Ԫ���ĵ��裬ijʵ��С�������˲������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ���ȹ�����ָϵͳ����������ȣ�Ҳ���������ȣ�������̲�����罻������ | |
| B�� | �������ڵ������ȴ��ݹ�����ϵͳ���ܱ仯�����ȣ����Բ���˵������ж���������ֻ��˵�������ջ�ų��������� | |
| C�� | ������Һ���е���ԽС����ijһ˲�������ײ��Һ�������Խ�٣�ײ�����õIJ�ƽ���Ծͱ��ֵ�Խ���ԣ���������˶�Խ���� | |
| D�� | ���صĶ����֪���ؽϴ�ĺ��״̬��������̶Ⱥ�С�ĺ��״̬��Ҳ���dz��ָ��ʽ�С�ĺ��״̬ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{x}_{1}}{{t}_{1}}$=$\frac{{x}_{2}}{{t}_{2}}$=$\frac{{x}_{3}}{{t}_{3}}$ | B�� | $\frac{{x}_{1}}{{t}_{1}}$��$\frac{{x}_{2}}{{t}_{2}}$��$\frac{{x}_{3}}{{t}_{3}}$ | ||
| C�� | $\frac{{x}_{1}}{{{t}_{1}}^{2}}$=$\frac{{x}_{2}}{{{t}_{2}}^{1}}$=$\frac{{x}_{3}}{{t}_{{3}^{2}}}$ | D�� | $\frac{{x}_{1}}{{{t}_{1}}^{2}}$��$\frac{{x}_{2}}{{{t}_{2}}^{1}}$��$\frac{{x}_{3}}{{t}_{{3}^{2}}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ͼ��ʾ����OΪԲ�ģ�MNΪֱ����Բ����벿�����д�ֱֽ���������ǿ�ų�����������������������ͬ����������ͬ�Ĵ���������a��b��c������ͬ�����ʷֱ���ao��bo��co����ֱ�ڴų�����ų�������֪ao��bo��co��bo�ļнǶ�Ϊ30�㣬a��b��c�������Ӵ�����ų�������ų�����ʱ��ֱ�Ϊta��tb��tc�������и�����ʱ���ϵ���ܵ��ǣ�������
��ͼ��ʾ����OΪԲ�ģ�MNΪֱ����Բ����벿�����д�ֱֽ���������ǿ�ų�����������������������ͬ����������ͬ�Ĵ���������a��b��c������ͬ�����ʷֱ���ao��bo��co����ֱ�ڴų�����ų�������֪ao��bo��co��bo�ļнǶ�Ϊ30�㣬a��b��c�������Ӵ�����ų�������ų�����ʱ��ֱ�Ϊta��tb��tc�������и�����ʱ���ϵ���ܵ��ǣ�������| A�� | ta��tb��tc | B�� | ta��tb��tc | C�� | ta=tb��tc | D�� | ta=tb=tc |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
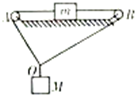 ����M��m�ֱ��ÿ���⻬�����ֵ�����������ͼ���ã�OA��OB��ˮƽ��ļнǷֱ�Ϊ53���37�㣬����M��m�������ֱ�Ϊ20N��10N��m��ˮƽ��Ķ�Ħ������Ϊ0.5��M��m�ij��ٶȶ�Ϊ�㣬������
����M��m�ֱ��ÿ���⻬�����ֵ�����������ͼ���ã�OA��OB��ˮƽ��ļнǷֱ�Ϊ53���37�㣬����M��m�������ֱ�Ϊ20N��10N��m��ˮƽ��Ķ�Ħ������Ϊ0.5��M��m�ij��ٶȶ�Ϊ�㣬������| A�� | ��OA��M��������СΪ12N | |
| B�� | ��OB��M��������СΪ16N | |
| C�� | m�ܵ�ˮƽ���Ħ������СΪ10N������ˮƽ���� | |
| D�� | m�ܵ�ˮƽ���Ħ������СΪ4N������ˮƽ���� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{3A}{16}$ | B�� | $\frac{7A}{16}$ | C�� | $\frac{11A}{16}$ | D�� | $\frac{13A}{16}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com