
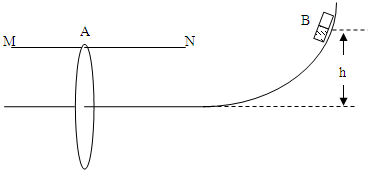
 如图所示,光滑弧形轨道和一足够长的光滑水平轨道相连,水平轨道上方有足够长的光滑绝缘体MN,上挂一光滑铝环A,在弧形轨道上高为h的地方无初速释放磁铁B(可视为质点),B下滑至水平轨道时恰沿A的中心轴线运动,设A、B的质量分别为MA、MB,求A获得最大速度和全过程中产生的电能.(忽略B沿弧形轨道下滑时环A产生的感应电流)
如图所示,光滑弧形轨道和一足够长的光滑水平轨道相连,水平轨道上方有足够长的光滑绝缘体MN,上挂一光滑铝环A,在弧形轨道上高为h的地方无初速释放磁铁B(可视为质点),B下滑至水平轨道时恰沿A的中心轴线运动,设A、B的质量分别为MA、MB,求A获得最大速度和全过程中产生的电能.(忽略B沿弧形轨道下滑时环A产生的感应电流) 阅读快车系列答案
阅读快车系列答案科目:高中物理 来源: 题型:
 (2011?江苏模拟)如图所示为放置在竖直平面内游戏滑轨的模拟装置,滑轨由四部分粗细均匀的金属杆组成,其中水平直轨AB与倾斜直轨CD长均为L=6m,圆弧形轨道AQC和BPD均光滑,AQC的半径为r=1m,AB、CD与两圆弧形轨道相切,O2D、O1C与竖直方向的夹角均为θ=37°.现有一质量为m=1kg的小球穿在滑轨上,以Ek0=24J的初动能从B点开始水平向左运动,小球与两段直轨道间的动摩擦因数均为μ=
(2011?江苏模拟)如图所示为放置在竖直平面内游戏滑轨的模拟装置,滑轨由四部分粗细均匀的金属杆组成,其中水平直轨AB与倾斜直轨CD长均为L=6m,圆弧形轨道AQC和BPD均光滑,AQC的半径为r=1m,AB、CD与两圆弧形轨道相切,O2D、O1C与竖直方向的夹角均为θ=37°.现有一质量为m=1kg的小球穿在滑轨上,以Ek0=24J的初动能从B点开始水平向左运动,小球与两段直轨道间的动摩擦因数均为μ=| 1 | 6 |
查看答案和解析>>
科目:高中物理 来源: 题型:
 (2010?上海模拟)如图所示为放置在竖直平面内游戏滑轨的模拟装置,滑轨由四部分粗细均匀的金属杆组成,其中倾斜直轨AB与水平直轨CD长均为L=3m,圆弧形轨道APD和BQC均光滑,BQC的半径为r=1m,APD的半径为R=2m,AB、CD与两圆弧形轨道相切,O2A、O1B与竖直方向的夹角均为θ=37°.现有一质量为m=1kg的小球穿在滑轨上,以Ek0的初动能从B点开始沿AB向上运动,小球与两段直轨道间的动摩擦因数均为μ=
(2010?上海模拟)如图所示为放置在竖直平面内游戏滑轨的模拟装置,滑轨由四部分粗细均匀的金属杆组成,其中倾斜直轨AB与水平直轨CD长均为L=3m,圆弧形轨道APD和BQC均光滑,BQC的半径为r=1m,APD的半径为R=2m,AB、CD与两圆弧形轨道相切,O2A、O1B与竖直方向的夹角均为θ=37°.现有一质量为m=1kg的小球穿在滑轨上,以Ek0的初动能从B点开始沿AB向上运动,小球与两段直轨道间的动摩擦因数均为μ=| 1 | 3 |
查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示为放置在竖直平面内游戏滑轨的模拟装置图,滑轨由四部分粗细均匀的金属杆组成,其中水平直轨AB与倾斜直轨CD两者的长L均为6m,圆弧形轨道AQC和BPD均光滑,AQC的半径r=1m,AB、CD与两圆弧形轨道相切,O2D、O1C与竖直方向的夹角θ均为37°.现有一质量m=1kg的小球穿在滑轨上,以30J的初动能Ek0从B点开始水平向右运动,小球与两段直轨道间的动摩擦因素μ均为
如图所示为放置在竖直平面内游戏滑轨的模拟装置图,滑轨由四部分粗细均匀的金属杆组成,其中水平直轨AB与倾斜直轨CD两者的长L均为6m,圆弧形轨道AQC和BPD均光滑,AQC的半径r=1m,AB、CD与两圆弧形轨道相切,O2D、O1C与竖直方向的夹角θ均为37°.现有一质量m=1kg的小球穿在滑轨上,以30J的初动能Ek0从B点开始水平向右运动,小球与两段直轨道间的动摩擦因素μ均为| 1 | 6 |
查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示为放置在竖直平面内游戏滑轨的模拟装置,滑轨由四部分粗细均匀的金属杆组成,其中倾斜直轨AB与水平直轨CD长均为L=3m,圆弧形轨道APD和BQC均光滑,AB、CD与两圆弧形轨道相切,BQC的半径为r=1m,APD的半径为R=2m,O2A、O1B与竖直方向的夹角均为θ=37°.现有一质量为m=1kg的小球穿在滑轨上,以Ek0的初动能从B点开始沿AB向上运动,小球与两段直轨道间的动摩擦因数均为μ=
如图所示为放置在竖直平面内游戏滑轨的模拟装置,滑轨由四部分粗细均匀的金属杆组成,其中倾斜直轨AB与水平直轨CD长均为L=3m,圆弧形轨道APD和BQC均光滑,AB、CD与两圆弧形轨道相切,BQC的半径为r=1m,APD的半径为R=2m,O2A、O1B与竖直方向的夹角均为θ=37°.现有一质量为m=1kg的小球穿在滑轨上,以Ek0的初动能从B点开始沿AB向上运动,小球与两段直轨道间的动摩擦因数均为μ=| 1 | 3 |
查看答案和解析>>
科目:高中物理 来源: 题型:
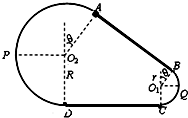 (2011?浙江模拟)如图所示为放置在竖直平面内游戏滑轨的模拟装置,滑轨由四部分粗细均匀的金属杆组成,其中倾斜直轨AB与水平直轨CD长均为L=3m,圆弧形轨道APD和BQC均光滑,BQC的半径为r=1m,APD的半径为R,AB、CD与两圆弧形轨道相切,O2A、O1B与竖直方向的夹角均为θ=370.现有一质量为m=1kg的小环穿在滑轨上,以某一初速度从B点开始沿AB向上运动,并恰能通过滑轨最高点.设小环与两段直轨道间的动摩擦因数均为μ=
(2011?浙江模拟)如图所示为放置在竖直平面内游戏滑轨的模拟装置,滑轨由四部分粗细均匀的金属杆组成,其中倾斜直轨AB与水平直轨CD长均为L=3m,圆弧形轨道APD和BQC均光滑,BQC的半径为r=1m,APD的半径为R,AB、CD与两圆弧形轨道相切,O2A、O1B与竖直方向的夹角均为θ=370.现有一质量为m=1kg的小环穿在滑轨上,以某一初速度从B点开始沿AB向上运动,并恰能通过滑轨最高点.设小环与两段直轨道间的动摩擦因数均为μ=| 1 |
| 3 |
| 10m |
| s2 |
| 1 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com