
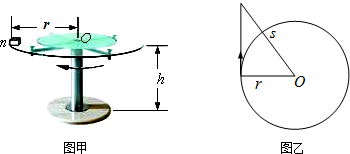
���� ��1���������ٶ������ڵĹ�ϵ������ٶȵĴ�С�����ݾ�Ħ�����ṩ���������Ħ�����Ĵ�С��
��2������ƽ���˶��Ĺ����������ij��ٶȣ�������Ħ�����ṩ���������ľ���������Ķ�Ħ��������
��� �⣺��1�����ٶȴ�С$v=\frac{2��r}{T}$��
ľ������Ħ��������ľ��������Բ���˶�����������$f=m{��\frac{2��}{T}��^2}r$ ��
��2��ľ�����벣������ƽ���˶����У�$h=\frac{1}{2}g{t^2}$��x=vt ��
x�����s���뾶r�Ĺ�ϵ��s2=r2+x2����$v=\sqrt{\frac{{��{s^2}-{r^2}��g}}{2h}}$��
�ɦ�mg=$\frac{m{v}^{2}}{r}$����$��=\frac{{{s^2}-{r^2}}}{2rh}$
�𣺣�1��������Բ���˶�������ΪT��ľ������ٶ���$\frac{2��r}{T}$������Ħ�����Ĵ�С��$m{��\frac{2��}{T}��}^{2}r$��
��2��ľ����ٶȴ�С��$\sqrt{\frac{��{s}^{2}-{r}^{2}��g}{2h}}$������벣�����Ķ�Ħ��������$\frac{{s}^{2}-{r}^{2}}{2rh}$��
���� ���⿼����Բ���˶���ƽ���˶����ۺϣ�����ƽ���˶���֪��ˮƽ�������ֱ�����ϵ��˶����ɣ�����Բ���˶���֪������������Դ�����ţ�ٵڶ����ɽ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�������
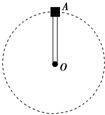 ��L=0.5m����ˣ���һ��������һ�����A��A������m=2kg������A����ֱƽ������O��������Բ���˶�����ͼ��ʾ����Aͨ����ߵ�ʱ�����������������A�Ը˵���������С��g=10m/s2����
��L=0.5m����ˣ���һ��������һ�����A��A������m=2kg������A����ֱƽ������O��������Բ���˶�����ͼ��ʾ����Aͨ����ߵ�ʱ�����������������A�Ը˵���������С��g=10m/s2�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | �³��Ĺ����������ij��������ϸ������������ij��� | |
| B�� | �ϸ��Ĺ����������ij��������³������������ij��� | |
| C�� | �ϸ����³������������ij�����С��ͬ | |
| D�� | �ϸ��Ĺ����и����ij��������³������и����ij��� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | 2m/s2 | B�� | 1.99m/s2 | C�� | 4m/s2 | D�� | 4.5m/s2 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
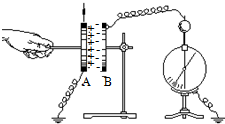 ijͬѧ������ͼ��ʾ��װ�����о�ƽ�а���������ݵ�Ӱ�����أ�
ijͬѧ������ͼ��ʾ��װ�����о�ƽ�а���������ݵ�Ӱ�����أ��鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �����˶�����ٶȷ���һ���ı� | |
| B�� | �������ɽǶȵ��ȱ���ֱ���˶��ĺ��˶�������ֱ���˶� | |
| C�� | ������������������Ϊ�㣬��е��һ�����غ� | |
| D�� | ����F=kQ1Q2/r2��֪����r��0ʱ��F���� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
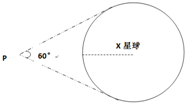 ij���տ���С���Э������������ʵ�飺
ij���տ���С���Э������������ʵ�飺�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com