
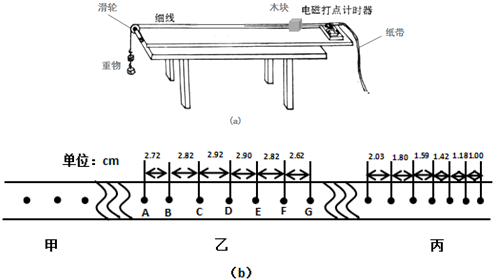
| A、点D处 | B、点C处 | C、CD段之间 | D、DE段之间. |
分析 (1)实验时应先启动打点计时器,再释放纸带.
(2)根据某段时间内的平均速度等于中间时刻的瞬时速度求出B点的速度,根据连续相等时间内的位移之差是一恒量,运用逐差法求出加速度.
(3)通过题目给出的数据作出速度-时间图象,解出其斜率即是小车的加速度.误差最小.
(4)根据相等时间内的位移变化,确定速度最大的位置.
解答 解:(1)开始实验时,应先启动打点计时器,再释放纸带.
(2)B点的瞬时速度${v}_{B}=\frac{{x}_{AC}}{2T}=\frac{(2.72+2.82)×1{0}^{-2}}{0.04}m/s$≈1.39m/s,
根据△x=aT2,运用逐差法得,$a=\frac{(1.42+1.18+1.00-2.03-1.80-1.59)×1{0}^{-2}}{9×0.0{2}^{2}}$m/s2≈-5.06m/s2.
(3)A、在处理实验数据时,如果只使用其中两个数据,由于偶然误差的存在可能会造成最后误差较大;所以我们可以根据实验数据画出v-t图象,考虑到误差,不可能是所有点都整齐的排成一条直线,连线时,应该尽量使那些不能画在线上的点均匀地分布在线的两侧,这样图线上会舍弃误差较大的点,由图线上任意两点所对应的速度及时间,用公式a=$\frac{△v}{△t}$算出加速度,所以误差小,故A错误,C正确.
B、根据实验数据画出v-t图象,当纵坐标取不同的标度时,图象的倾角就会不同,所以量出其倾角,用公式a=tanα算出的数值并不是加速度,故B错误.
D、方法D也具有方法A相同的缺点,比如求解时,${a}_{1}=\frac{{v}_{2}-{v}_{1}}{T}$,${a}_{2}=\frac{{v}_{3}-{v}_{2}}{T}$,…${a}_{5}=\frac{{v}_{6}-{v}_{5}}{T}$,然后算出平均值a,求平均值时,$a=\frac{{v}_{6}-{v}_{1}}{5T}$,只用了v6和v1两组数据,偶然误差较大,故D错误.
故选:C.
(4)速度越来越大,相等时间内的位移越来越大,由于CD段的位移最大,则最大速度可能出现在乙纸带的CD段之间,故选:C.
故答案为:(1)先启动打点计时器,再释放纸带;(2)1.39,5.06,(3)C,(4)C.
点评 在实验中处理数据的方法较多,而图象法往往是一种比较准确的解题方法.以及掌握纸带的处理方法,会通过纸带求解瞬时速度和加速度,关键是匀变速直线运动推论的运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中物理 来源: 题型:选择题
 用不同频率光照射某一金属发生光电效应时,光电子逸出最大初动能随入射光频率变化的图象如图所示,则图中横、纵轴截距及斜率的物理意义为( )
用不同频率光照射某一金属发生光电效应时,光电子逸出最大初动能随入射光频率变化的图象如图所示,则图中横、纵轴截距及斜率的物理意义为( )| A. | 斜率为普朗克常数的倒数 | B. | 纵轴截距为逸出功的倒数 | ||
| C. | 横轴截距为极限频率 | D. | 横轴截距为极限波长 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 木星绕太阳运动的周期和轨道半径 | |
| B. | 木星绕太阳运动的周期和木星的半径 | |
| C. | 木星的卫星绕木星运动的周期和轨道半径 | |
| D. | 木星的卫星绕木星运动的周期和木星的半径 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | lg$\frac{a}{{a}_{0}}$=2lg$\frac{{R}_{0}}{R}$ | B. | lg$\frac{a}{{a}_{0}}$=$\frac{1}{2}$lg$\frac{{R}_{0}}{R}$ | C. | lg$\frac{v}{{v}_{0}}$=$\frac{1}{2}$lg$\frac{{R}_{0}}{R}$ | D. | lg$\frac{v}{{v}_{0}}$=$\frac{1}{2}$lg$\frac{R}{{R}_{0}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 该星球表面的重力加速度与地球表面重力加速度之比为1:9 | |
| B. | 该星球的密度与地球密度之比为4:9 | |
| C. | 该星球与地球第一宇宙速度之比为3:2 | |
| D. | 在该星球与地球上自相同高度处以相同初速度平抛物体的水平射程之比为1:1 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:计算题
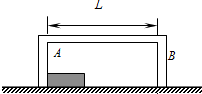 有一尺寸可忽略的木块放在足够长的水平粗糙地面上.取一无盖的长方形木盒B开口向下将A罩住.B的左右内壁间的距离为L=2m.开始时,A与B的左内壁相接触(如图所示),两者以相同的初速度v0向右,在摩擦力作用下,分别以大小为1m/s2和2m/s2的加速度做匀减速直线运动.若A和B能相撞.则相撞的结果是两者交换速度 (即撞后瞬间A和B的速度分别等于撞前瞬间B和A的速度,且撞击所用的时间极短可以忽略).A与B的其他侧面之间均无接触.重力加速度为g.
有一尺寸可忽略的木块放在足够长的水平粗糙地面上.取一无盖的长方形木盒B开口向下将A罩住.B的左右内壁间的距离为L=2m.开始时,A与B的左内壁相接触(如图所示),两者以相同的初速度v0向右,在摩擦力作用下,分别以大小为1m/s2和2m/s2的加速度做匀减速直线运动.若A和B能相撞.则相撞的结果是两者交换速度 (即撞后瞬间A和B的速度分别等于撞前瞬间B和A的速度,且撞击所用的时间极短可以忽略).A与B的其他侧面之间均无接触.重力加速度为g.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com