
 一个半径为R、半球形的光滑碗固定不动.碗口处于水平面内.
一个半径为R、半球形的光滑碗固定不动.碗口处于水平面内.分析 (1)由机械能守恒定律即可求解速度;
(2)根据平均功率$\overline{P}=\frac{W}{t}$求出高度,再由机械能守恒定律即可求解;
(3)竖直方向瞬时功率Pt=mgvy,再根据几何关系即可求解;
(4)速度最大处即为其轨迹的最低点,此处小球无沿球面向下的速度分量,再根据动能定理列式即可求解.
解答 解:(1)由机械能守恒定律有:$\frac{1}{2}mv_m^2=mgR$
解得:${v_m}=\sqrt{2gR}$
(2)平均功率$\overline P=\frac{mgh}{t}$,解得 $h=\frac{\overline Pt}{mg}$
由机械能守恒定律有:$\frac{1}{2}mv_t^2=mgh$
t时间末瞬时速度${v_t}=\sqrt{2gh}=\sqrt{2g\frac{\overline Pt}{mg}}=\sqrt{\frac{2\overline Pt}{m}}$
(3)竖直方向瞬时功率Pt=mgvy
而 ${v}_{y}={v}_{t}sinθ={v}_{t}×\frac{\sqrt{{R}^{2}-{h}^{2}}}{{R}^{\;}}=\sqrt{\frac{2\overline{P}t}{m}}×\frac{\sqrt{{R}^{2}-{h}^{2}}}{{R}^{\;}}$
解得:${P_t}=\sqrt{\frac{{2\overline Pt({m^2}{g^2}{R^2}-{{\overline P}^2}{t^2})}}{{m{R^2}}}}$
(4)速度最大处即为其轨迹的最低点,此处小球无沿球面向下的速度分量.则小球速度就是vx=$\frac{v_0}{cosθ}$,
根据动能定理(或机械能守恒)
$mgRsinθ=\frac{1}{2}mv_x^2-\frac{1}{2}mv_0^2$
联立上两式得${v_0}=\sqrt{3gR}$
答:(1)若将小球静止从碗口内侧释放,运动中能达到的最大速度为$\sqrt{2gR}$;
(2)若将质量m的小球静止从碗口内侧释放,从释放开始计时,t时间内重力的平均功率$\overline{P}$,小球尚未到达碗底,则t时间末小球的瞬时速度为$\sqrt{\frac{2\overline{P}t}{m}}$;
(3)求在上问中t时间末小球重力的瞬时功率为$\sqrt{\frac{2\overline{P}t({m}^{2}{g}^{2}{R}^{2}-{\overline{P}}^{2}{t}^{2})}{m{R}^{2}}}$;
(4)释放初速度为$\sqrt{3gR}$.
点评 本题主题考查了机械能守恒定律、动能定理以及平均功率和瞬时功率的计算,过程较为复杂,难度适中.


科目:高中物理 来源: 题型:多选题
 两根足够长的光滑导轨竖直放置,间距为L,底端接阻值为R的电阻.将质量为m的金属棒悬挂在一个固定的轻弹簧下端,金属棒和导轨接触良好,导轨所在平面与磁感应强度为B的匀强磁场垂直,如图所示.除电阻R外其余电阻不计.现将金属棒从弹簧原长位置由静止释放,则( )
两根足够长的光滑导轨竖直放置,间距为L,底端接阻值为R的电阻.将质量为m的金属棒悬挂在一个固定的轻弹簧下端,金属棒和导轨接触良好,导轨所在平面与磁感应强度为B的匀强磁场垂直,如图所示.除电阻R外其余电阻不计.现将金属棒从弹簧原长位置由静止释放,则( )| A. | 金属棒向下运动时,流过电阻R的电流方向为a→b | |
| B. | 释放瞬间金属棒的加速度等于重力加速度g | |
| C. | 金属棒的速度为v时,所受的安培力大小为F=$\frac{{B}^{2}{L}^{2}v}{R}$ | |
| D. | 电阻R上产生的总热量等于金属棒重力势能的减少 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
 质量为m的物块始终相对静止在倾角为θ的斜面上,如图所示.若斜面向左匀速移动距离s,斜面对物体做功为0;若斜面向上匀速移动距离s,则斜面对物体做功为mgs.
质量为m的物块始终相对静止在倾角为θ的斜面上,如图所示.若斜面向左匀速移动距离s,斜面对物体做功为0;若斜面向上匀速移动距离s,则斜面对物体做功为mgs.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 垒球落地时的瞬时速度的大小 | B. | 垒球落地时的瞬时速度的方向 | ||
| C. | 垒球在空中运动的时间 | D. | 垒球在空中运动的水平位移 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 用多用表测量一个定值电阻的阻值.
用多用表测量一个定值电阻的阻值.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图,某人用一根轻绳通过定滑轮牵拉一个置于水平面上的一艘小船,当人以速度v匀速向右运动时,则( )
如图,某人用一根轻绳通过定滑轮牵拉一个置于水平面上的一艘小船,当人以速度v匀速向右运动时,则( )| A. | 小船作匀速运动 | B. | 图示时刻,小船的速度为2v | ||
| C. | 小船作匀减速运动 | D. | 小船作匀加速运动 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
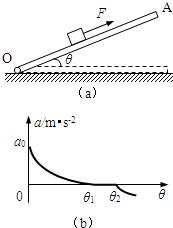 如图(a)所示,木板OA可绕轴O在竖直平面内转动,某研究小组利用此装置探索物块在方向始终平行于斜面、大小为F=8N的力作用下由静止释放后加速度与斜面倾角的关系.已知物块的质量m=1kg,通过DIS实验,得到如图(b)所示的加速度与斜面倾角的关系图线.若物块与木板间的动摩擦因数为0.2,假定物块与木板间的最大静摩擦力始终等于滑动摩擦力,g取10m/s2.试问:
如图(a)所示,木板OA可绕轴O在竖直平面内转动,某研究小组利用此装置探索物块在方向始终平行于斜面、大小为F=8N的力作用下由静止释放后加速度与斜面倾角的关系.已知物块的质量m=1kg,通过DIS实验,得到如图(b)所示的加速度与斜面倾角的关系图线.若物块与木板间的动摩擦因数为0.2,假定物块与木板间的最大静摩擦力始终等于滑动摩擦力,g取10m/s2.试问:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 由3节动车加3节拖车编成的 | B. | 由3节动车加9节拖车编成的 | ||
| C. | 由6节动车加2节拖车编成的 | D. | 由3节动车加4节拖车编成的 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com