
| A�� | �ڹ��ЧӦʵ���У���ͬ��Ƶ�ʵĹ����䲻ͬ�Ľ������棬�ӽ��������ݳ��Ĺ���ӵ���������EkԽ�������ֽ������ݳ���W0ԽС | |
| B�� | һȺ����n=5�ܼ�����ԭ������ܼ�ԾǨʱ�ܷ����10�ֲ�ͬƵ�ʵĹ� | |
| C�� | �����ߡ������ߺͦ����������ֲ�����ͬ�ĵ�Ų� | |
| D�� | 14��������Ԫ�ص�ԭ�Ӻ��ھ���һ����˥�ں�һ����7��ԭ�Ӻ˷���˥�� |
���� ���ݹ��ЧӦ���̣�ץס������Ƶ����ȣ�ͨ���������ܲ�ͬ���ȽϽ������ݳ�����������ѧ��Ϲ�ʽ��ȷ��һȺ����n=5�ܼ�����ԭ������ܼ�ԾǨʱ�ܷ������ͬƵ�ʹ��ӵ��������������Ǻ��������������ǵ��������������ǵ�Ų�����˥�ھ���ͳ�ƹ��ɣ��Դ�����ԭ�Ӻ����ã�
��� �⣺A�����ݹ��ЧӦ����Ekm=hv-W0֪����ͬ��Ƶ�ʵĹ����䲻ͬ�Ľ������棬�ӽ��������ݳ��Ĺ���ӵ���������EkԽ�������ֽ������ݳ���W0ԽС����A��ȷ��
B������${C}_{5}^{2}=10$֪��һȺ����n=5�ܼ�����ԭ������ܼ�ԾǨʱ�ܷ����10�ֲ�ͬƵ�ʵĹ⣬��B��ȷ��
C���������Ǻ��������������ǵ��������������ǵ�Ų�����C����
D����˥�ھ���ͳ�ƹ��ɣ��Դ�����ԭ�Ӻ����ã���������ԭ�Ӻ˲����ã���D����
��ѡ��AB��
���� ���⿼���˹��ЧӦ���̡����ߵ�ʵ�ʡ���˥�ڵȻ���֪ʶ�㣬�ؼ�Ҫ��Ϥ�̲ģ��μ���Щ�������ɺͻ���������ܻ�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | -3 km-4 km | B�� | -3 km 4 km | C�� | 3 km-4 km | D�� | 3 km 4 km |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ����������嶯���� | B�� | �ٶȴ�����嶯���� | ||
| C�� | �����ķ������ٶȵķ�����ͬ | D�� | �����ķ���������ٶȷ����෴ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ͼ��
 ��ͼ��ʾ���ʵ�P�ܵ����������������ã�F1=20N��F2=50N��F3=40N��F1��F2��һ��ֱ��������F3��ֱ��
��ͼ��ʾ���ʵ�P�ܵ����������������ã�F1=20N��F2=50N��F3=40N��F1��F2��һ��ֱ��������F3��ֱ���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� | 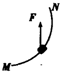 | C�� | 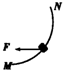 | D�� | 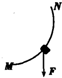 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
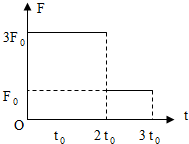 ����Ϊm�����徲ֹ�ڹ⻬ˮƽ���ϣ���t=0ʱ�̿�ʼ�ܵ�ˮƽ�������ã����Ĵ�СF��ʱ��t�Ĺ�ϵ��ͼ��ʾ�����ķ��ֲ��䣬������
����Ϊm�����徲ֹ�ڹ⻬ˮƽ���ϣ���t=0ʱ�̿�ʼ�ܵ�ˮƽ�������ã����Ĵ�СF��ʱ��t�Ĺ�ϵ��ͼ��ʾ�����ķ��ֲ��䣬������| A�� | 3t0ʱ�̵�˲ʱ����Ϊ$\frac{{5F_0^2{t_0}}}{m}$ | |
| B�� | 3t0ʱ�̵�˲ʱ����Ϊ$\frac{{7F_0^2{t_0}}}{m}$ | |
| C�� | ��t=0��3t0���ʱ���ڣ�ˮƽ����ƽ������Ϊ$\frac{{49F_0^2{t_0}}}{6m}$ | |
| D�� | ��t=0��3t0���ʱ���ڣ�ˮƽ����ƽ������Ϊ$\frac{{25F_0^2{t_0}}}{6m}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{\frac{g��{r}^{2}-{R}^{2}��}{2h{R}^{2}}}$ | B�� | $\sqrt{\frac{g��{r}^{2}-{R}^{2}��}{2h{r}^{2}}}$ | C�� | $\sqrt{\frac{g��{r}^{2}-{R}^{2}��}{h{R}^{2}}}$ | D�� | $\sqrt{\frac{g��{r}^{2}-{R}^{2}��}{h{r}^{2}}}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com