Question

10．如图甲所示，真空中竖直放置两块相距为d的平行金属板P、Q．两板间加上如图乙所示最大值为U₀的周期性变化的电压，在Q板右侧某个区域内存在磁感应强度大小为B、方向垂直于纸面向里的有界匀强磁场．在紧靠P板处有粒子源A，自t=0开始连续释放初速不计的粒子，经一段时间从Q板小孔O射入磁场，射出磁场时所有粒子的速度方向均竖直向上．已知粒子质量为m，电荷量为+q，不计粒子重力及相互间的作用力，电场变化周期T=3d$\sqrt{\frac{2m}{q{U}_{0}}}$．试求：
（1）t=0时刻释放的粒子在P、Q间运动的时间．
（2）粒子射入磁场时的最大速率和最小速率．
（3）有界磁场区域的最小面积．

Answer 1

分析 （1）带电粒子在电场中加速，牛顿第二定律和运动学公式即可求解粒子在P、Q间运动的时间；
（2）粒子在电场中加速，电场力做功，由动能定理即可求出粒子射入磁场时的最大速率和最小速率；
（3）射出磁场时所有粒子的速度方向均竖直向上，做出运动的轨迹图，即可几何关系即可求解．

解答 解：（1）设t=0时刻释放的粒子在$\frac{T}{3}$时间内一直做匀加速直线运动，其加速度大小为a，位移为x，则由牛顿第二定律、电场力公式和运动学公式得．
$q\frac{{U}_{0}}{d}=ma$，
x=$\frac{1}{2}a{t}^{2}$，
解得：a=$\frac{q{U}_{0}}{md}$．
$x=\frac{1}{2}•\frac{q{U}_{0}}{md}（\frac{1}{3}T）^{2}$=$\frac{1}{2}\frac{q{U}_{0}}{md}（d\sqrt{\frac{2m}{q{U}_{0}}}）^{2}=d$．
可见，该粒子在$\frac{T}{3}$时间内恰好运动到O处，该粒子在P、Q间运动的时间为：
t=$\frac{1}{3}T$=$d\sqrt{\frac{2m}{q{U}_{0}}}$．

（2）分析可知，在t=0时刻释放的粒子一直在电场中加速，对应进入磁场时的速率最大．
设最大速率为v_max，由运动学公式得，
${v}_{max}=a\frac{1}{3}T=\sqrt{\frac{2q{U}_{0}}{m}}$．
设在t₁时刻释放的粒子先做匀加速直线运动，经△t后，再做匀速直线运动，在T时间恰好由小孔O射入磁场．设此时粒子的速度大小为v₁，则由运动学公式得：$\frac{1}{2}a△{t}^{2}+a△t×\frac{2}{3}T=\frac{1}{2}a（\frac{1}{3}T）^{2}$，
v₁=a△t，
解得：$△t=\frac{\sqrt{5}-2}{3}T$．
${v}_{1}=a•△t=（\sqrt{5}-2）\sqrt{\frac{2q{U}_{0}}{m}}$．
由由图可知，在t₁至$\frac{T}{3}$时间内某时刻进入电场的粒子，其运动过程为先加速、后匀速，再加速，当速度达到v₁=a△t时，粒子还未运动到小孔O处．图中阴影的面积等于粒子此刻到小孔的距离；粒子需再经加速后方可到达O处，此时速度已大于v₁．所以，速率v₁是粒子进入磁场时的最小速率，即：
v_min=$（\sqrt{5}-2）\sqrt{\frac{2q{U}_{0}}{m}}$．

（3）粒子进入磁场后做轨迹为四分之一圆周的运动，设轨迹半径为r，根据向心力公式和洛伦兹力公式得：$qvB=m\frac{{v}^{2}}{r}$，
解得：r=$\frac{mv}{qB}$．
最大速率对应的半径为：${r}_{max}=\sqrt{\frac{2m{U}_{0}}{q{B}^{2}}}$，
最小速率对应的半径为：${r}_{min}=（\sqrt{5}-2）\sqrt{\frac{2m{U}_{0}}{q{B}^{2}}}$．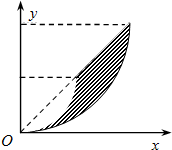
分析可知，当左、右边界为最小半径、最大半径对应的四分之一圆周，上边界y=x的一部分时，磁场区域的面积最小，如图所示，设面积为S，则由几何关系可得：
$S=（\frac{1}{4}π{{r}_{min}}^{2}-\frac{1}{2}{{r}_{max}}^{2}）-$$（\frac{1}{4}π{{r}_{min}}^{2}-\frac{1}{2}{{r}_{min}}^{2}）$=$\frac{π-2}{4}（{{r}_{max}}^{2}-{{r}_{min}}^{2}）$，
解得：S=$（2\sqrt{5}-4）（π-2）\frac{m{U}_{0}}{q{B}^{2}}$．
答：（1）t=0时刻释放的粒子在P、Q间运动的时间为$d\sqrt{\frac{2m}{q{U}_{0}}}$．
（2）粒子射入磁场时的最大速率和最小速率分别为$\sqrt{\frac{2q{U}_{0}}{m}}、（\sqrt{5}-2）\sqrt{\frac{2q{U}_{0}}{m}}$．
（3）有界磁场区域的最小面积为$（2\sqrt{5}-4）（π-2）\frac{m{U}_{0}}{q{B}^{2}}$．

点评 考查粒子在电场中加速和在磁场中圆周运动问题，结合牛顿第二定律与几何关系来综合应用，掌握运动轨迹的半径公式．