
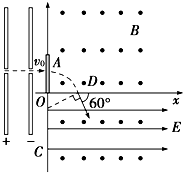
 ��ʵ���������ͼ��ʾ����y����ҷ���һ�Ÿ�Ӧǿ��ΪB�ķ���ֱֽ���������ǿ�ų�����x����·���һ��ǿΪE�ķ���ƽ��x�����ҵ���ǿ�糡����һǦ�������y�ᴦ������ֽ�洹ֱ������һ����Ϊm�������Ϊq�����ӣ������������ɾ�ֹ�������ٵ�ѹΪU�ĵ糡���٣�Ȼ���Դ�ֱ��Ǧ��ķ����A����ֱ�ߴ���Ǧ�壬�����x���ϵ�D������x������н�Ϊ60��ķ������糡�ʹų����ӵ��������y���ϵ�C�㣮��֪OD��Ϊl����
��ʵ���������ͼ��ʾ����y����ҷ���һ�Ÿ�Ӧǿ��ΪB�ķ���ֱֽ���������ǿ�ų�����x����·���һ��ǿΪE�ķ���ƽ��x�����ҵ���ǿ�糡����һǦ�������y�ᴦ������ֽ�洹ֱ������һ����Ϊm�������Ϊq�����ӣ������������ɾ�ֹ�������ٵ�ѹΪU�ĵ糡���٣�Ȼ���Դ�ֱ��Ǧ��ķ����A����ֱ�ߴ���Ǧ�壬�����x���ϵ�D������x������н�Ϊ60��ķ������糡�ʹų����ӵ��������y���ϵ�C�㣮��֪OD��Ϊl�������� ��1�������ڵ糡�м��٣��ɶ��ܶ�����������ٶȣ�
��2�����Ӹյ���Ǧ���ٶ����ɼ��ٵ糡���ٻ�õģ����ݶ��ܶ�����⣮����Ǧ�������������Բ���˶������ݼ��ι�ϵ������켣�뾶���Ӷ��������������ṩ��������������Ӵ���Ǧ�����ٶȣ�
��3���ɶ��ܶ�������������ӵ��ٶȣ�
��� �⣺��1�������ڵ糡�м��٣��ɶ��ܶ����ã�
qU=$\frac{1}{2}$mv02����ã�v0=$\sqrt{\frac{2qU}{m}}$��
��2�������ڴų���������Բ���˶���
��ţ�ٵڶ����ɵã�qvB=m$\frac{{v}^{2}}{R}$����ã�v=$\frac{qBR}{m}$��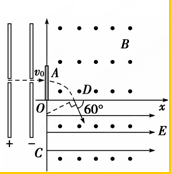
�����˶��켣��ͼ��ʾ���ɼ���֪ʶ�ã�sin60��=$\frac{l}{R}$��
��ã�R=$\frac{2l}{\sqrt{3}}$��v=$\frac{2qBl}{\sqrt{3}m}$��
�������������������Ӵ���Ǧ���Ķ��ܣ�EK=$\frac{1}{2}$mv2=$\frac{2{q}^{2}{B}^{2}{l}^{2}}{3m}$��
���Ӵ���Ǧ����ʧ�Ķ��ܣ���EK=EK0-EK=qU-$\frac{2{q}^{2}{B}^{2}{l}^{2}}{3m}$��
��3����D��Cֻ�е糡���������������ɶ��ܶ����ã�
-qEl=$\frac{1}{2}$mvC2-$\frac{1}{2}$mv2����ã�vC=$\sqrt{\frac{4{q}^{2}{B}^{2}{l}^{2}}{3{m}^{2}-\frac{2qEl}{m}}}$��
�𣺣�1�����Ӿ������ٵ糡����ٶ�Ϊ$\sqrt{\frac{2qU}{m}}$��
��2�����Ӿ���Ǧ��ʱ��ʧ�Ķ���ΪqU-$\frac{2{q}^{2}{B}^{2}{l}^{2}}{3m}$��
��3�����ӵ���C��ʱ���ٶ�Ϊ��$\sqrt{\frac{4{q}^{2}{B}^{2}{l}^{2}}{3{m}^{2}-\frac{2qEl}{m}}}$��
���� ���⿼����������ڵ糡��ų����ۺ�Ӧ�ã����ݶ��ܶ��������ٻ�õ��ٶȣ����ݼ���֪ʶ����ų��й켣�뾶�ȵȶ��dz��õķ������ر�Ҫע����������ڴų�����������ʼ�ղ����������ڵ糡�е糡��������·���أ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ������
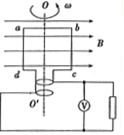 ���������ת����n����Ȧ��ÿ����Ȧ��Χ���ΪS����ǿ�ų��ĴŸ�Ӧǿ��ΪB������ת���Ľ��ٶ�Ϊ�أ���Ȧ����Ϊr�����·����ΪR������Ȧ����������ʱ��ʼ��ʱ����ʱ������ת��180������У���
���������ת����n����Ȧ��ÿ����Ȧ��Χ���ΪS����ǿ�ų��ĴŸ�Ӧǿ��ΪB������ת���Ľ��ٶ�Ϊ�أ���Ȧ����Ϊr�����·����ΪR������Ȧ����������ʱ��ʼ��ʱ����ʱ������ת��180������У����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
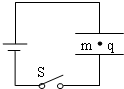 ��ͼ��ʾ��������Ϊd��ƽ�а��������һ��Դ���ӣ�����S�պϣ��������������һ����Ϊm���������Ϊq������ֹ������������������ȷ���ǣ�������
��ͼ��ʾ��������Ϊd��ƽ�а��������һ��Դ���ӣ�����S�պϣ��������������һ����Ϊm���������Ϊq������ֹ������������������ȷ���ǣ�������| A�� | ������������ | |
| B�� | ��Դ�綯�ƵĴ�С����$\frac{mgd}{q}$ | |
| C�� | �Ͽ�����S���ѵ����������������������������������˶� | |
| D�� | ���ֿ���S�պϣ��ѵ����������������������������������˶� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 һ������Ϊ50kg���ˣ�վ����ֱ�����˶��ŵ��������ذ��ϣ��������������ڹ�������ĵ��ɳӵ�ʾ��Ϊ40N����֪���ɳ��¹��ŵ����������Ϊ50N��ȡg=10m/s2������˵����ȷ���ǣ�������
һ������Ϊ50kg���ˣ�վ����ֱ�����˶��ŵ��������ذ��ϣ��������������ڹ�������ĵ��ɳӵ�ʾ��Ϊ40N����֪���ɳ��¹��ŵ����������Ϊ50N��ȡg=10m/s2������˵����ȷ���ǣ�������| A�� | �ذ���˵�֧����Ϊ600N | B�� | �ذ���˵�֧����Ϊ400N | ||
| C�� | �˵�����С��500N | D�� | �˴���ʧ��״̬ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
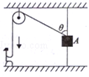 ��������ͨ���⻬����������ֹ�ڵ����ϵ�����A��A���ڹ⻬����ֱ���ϵ������ٶ�v��ֱ������������ʹ����Ϊm������A�����߶�h����ͼ��ʾλ��ʱ��ʱ������ֱ�˵ļн�Ϊ�ȣ���֪�������ٶ�Ϊg��������˵����ȷ���ǣ�������
��������ͨ���⻬����������ֹ�ڵ����ϵ�����A��A���ڹ⻬����ֱ���ϵ������ٶ�v��ֱ������������ʹ����Ϊm������A�����߶�h����ͼ��ʾλ��ʱ��ʱ������ֱ�˵ļн�Ϊ�ȣ���֪�������ٶ�Ϊg��������˵����ȷ���ǣ�������| A�� | ��ʱ����A���ٶ�Ϊ$\frac{v}{cos��}$ | |
| B�� | ��ʱ����A���ٶ�Ϊvcos�� | |
| C�� | �ù�������������A���Ĺ�Ϊmgh+$\frac{1}{2}$mv2 | |
| D�� | �ù�������������A���Ĺ�Ϊmgh+$\frac{1}{2}$mv2cos2 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
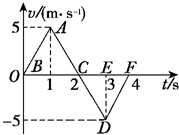
| A�� | t=1sʱ��ԭ����Զ | B�� | t=2sʱ��ԭ����Զ | ||
| C�� | t=3sʱ�ص�ԭ�� | D�� | t=4sʱ�ص�ԭ�㣬·��Ϊ20m |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 �������ͼ��ʾ����·�е���������ѹ��������Ե�·��Ӱ�첻�ƣ��պϿ��غ�����ƬP����ʱ��������
�������ͼ��ʾ����·�е���������ѹ��������Ե�·��Ӱ�첻�ƣ��պϿ��غ�����ƬP����ʱ��������| A�� | �ס�����ͼ�еĵ�ѹ����������С | |
| B�� | �ס�����ͼ�еĵ��������������� | |
| C�� | ��ͼ�еĵ�ѹ��������С����ͼ�еĵ�ѹ���������� | |
| D�� | ��ͼ�еĵ�����������С����ͼ�еĵ������������� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com