
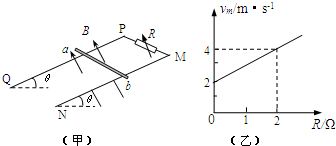
���� ��1�������˴Ӿ�ֹ��ʼ�������ٶȼ�С�ı�����˶�������������˶�����������֧�����Ͱ�������ƽ�⣬����ƽ�������Ƶ��� ����ٶ�vm��R�Ĺ�ϵ����ʽ���ͼ�������
��2�����ݹ��ܹ�ϵ�������������»�ʱ���������ĵ繦�ʵ����ֵPm��
��3����������Rȡ4��������ͼ��õ�����ٶȣ�Ȼ�����иʽ�͵繦�ʱ���ʽ������
��� �⣺��1����·���ܵ��裺R��=R+r
���ݱպϵ�·ŷķ���ɣ�������
I=$\frac{BLv}{R+r}$
���ﵽ����ٶ�ʱ��ƽ�⣬�У�
mgsin��=BIL+��mgcos��=$\frac{{B}^{2}{L}^{2}{v}_{m}}{R+r}$+��mgcos��
����vm=$\frac{mg��sin��-��cos�ȣ���R+r��}{{B}^{2}{L}^{2}}$=$\frac{m��10����sin30��-\frac{\sqrt{3}}{6}��cos30�㣩����R+r��}{0��{5}^{2}��{2}^{2}}$=2.5m��R+r��
ͼ���б�� k=1�����2.5m=1��m=0.4kg
����ؾ� b=2����� 2.5mr=2���� r=2��
��2�������������»�ʱ�����ȶ�����ΪI��
����ƽ��������
mgsin��=BIL+��mgcos��
�� I=$\frac{mg��sin��-��cos�ȣ�}{BL}$=$\frac{4����sin30��-\frac{\sqrt{3}}{6}��cos30�㣩}{0.5��2}$A=1A
�ʽ����������»�ʱ���������ĵ繦�ʵ����ֵ Pm=I2Rm=12��4W=4W
��3�������⣺E=BLv��P=$\frac{{E}^{2}}{R+r}$
�� P=$\frac{{B}^{2}{L}^{2}{v}^{2}}{R+r}$
���P=$\frac{{B}^{2}{L}^{2}{v}_{2}^{2}}{R+r}$-$\frac{{B}^{2}{L}^{2}{v}_{1}^{2}}{R+r}$
�ɶ��ܶ����ã�
W=$\frac{1}{2}m{v}_{2}^{2}$-$\frac{1}{2}m{v}_{1}^{2}$
������ W=$\frac{m��R+r��}{2{B}^{2}{L}^{2}}��$P=$\frac{0.4����4+2��}{2��0��{5}^{2}��{2}^{2}}��$1J=1.2J
��
��1�������˵�����m�ǣ�0.4kg����ֵr��2����
��2�������������»�ʱ���������ĵ繦�ʵ����ֵPm��4W��
��3����R=4��ʱ�����Ÿ�ab�»���·˲ʱ�繦��ÿ����1W�Ĺ����к������Ը����Ĺ�W��1.2J��
���� ����ؼ�����ȷ�����������������˶����ɣ�Ȼ������иʽ��ţ�ٵڶ����ɡ��繦�ʱ���ʽ��ʽ������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ͼ��ʾ���ڹ⻬��Ե��ˮƽ���Ϸ��������������෴��ˮƽ�������ǿ�ų���PQΪ���ų��ı߽磬�ų���Χ�㹻�Ÿ�Ӧǿ�ȵĴ�С�ֱ�ΪB1=B��B2=2B��һ����ֱ���õı߳�Ϊa������Ϊm������ΪR�������ν����߿��Գ��ٶ�v��ֱ�ų������ͼ��ʵ��λ�ÿ�ʼ�����˶������߿��˶�����ÿ���ų��и���һ������ʱ���߿���ٶ�Ϊ$\frac{v}{2}$���������ж���ȷ���ǣ�������
��ͼ��ʾ���ڹ⻬��Ե��ˮƽ���Ϸ��������������෴��ˮƽ�������ǿ�ų���PQΪ���ų��ı߽磬�ų���Χ�㹻�Ÿ�Ӧǿ�ȵĴ�С�ֱ�ΪB1=B��B2=2B��һ����ֱ���õı߳�Ϊa������Ϊm������ΪR�������ν����߿��Գ��ٶ�v��ֱ�ų������ͼ��ʵ��λ�ÿ�ʼ�����˶������߿��˶�����ÿ���ų��и���һ������ʱ���߿���ٶ�Ϊ$\frac{v}{2}$���������ж���ȷ���ǣ�������| A�� | �˹�����ͨ���߿����ĵ���Ϊ$\frac{3B{a}^{2}}{2R}$ | |
| B�� | �˹������߿�˷����������Ĺ�Ϊ$\frac{3}{8}$mv2 | |
| C�� | ��ʱ�߿�ļ��ٶ�Ϊ$\frac{9{B}^{2}{a}^{2}v}{2mR}$ | |
| D�� | ��ʱ�߿��еĵ繦��Ϊ$\frac{9{B}^{2}{a}^{2}{v}^{2}}{2R}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
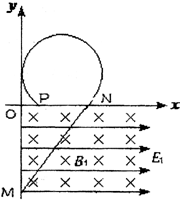 ��ͼ��ʾ����x���·������������ĵ糡��ų����糡������x�������糡ǿ�ȴ�СΪE1���ų�����ֱֽ������Ÿ�Ӧǿ�ȴ�СΪB1��һ������m=3g�������q=2��10-3 C�Ĵ�����С����y���ϵ�M����ֱ�������˶���x���ϵ�N�㣬�ٶȴ�Сv=5 m/s��������ˮƽ����ɦ�=53��ǣ�����֪OM=4 m����x���Ϸ�������������ǿ�糡E2����ǿ�ų�B2��ͼ�о�δ��������С����x���Ϸ���Բ���˶���ǡ����y�����У��˶��켣��ͼ��ʾ����g=10 m/s2��sin53��=0.8����
��ͼ��ʾ����x���·������������ĵ糡��ų����糡������x�������糡ǿ�ȴ�СΪE1���ų�����ֱֽ������Ÿ�Ӧǿ�ȴ�СΪB1��һ������m=3g�������q=2��10-3 C�Ĵ�����С����y���ϵ�M����ֱ�������˶���x���ϵ�N�㣬�ٶȴ�Сv=5 m/s��������ˮƽ����ɦ�=53��ǣ�����֪OM=4 m����x���Ϸ�������������ǿ�糡E2����ǿ�ų�B2��ͼ�о�δ��������С����x���Ϸ���Բ���˶���ǡ����y�����У��˶��켣��ͼ��ʾ����g=10 m/s2��sin53��=0.8�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ��ˮƽ���ڵ�������ABCD�ı߳�Ϊ2R������Ϊm�������Ϊ+q�����ӣ��������ƣ���AD�ߵ��е���ijһ���ٶȽ��������������������������ڼӷ�����ADƽ�С���СΪE����ǿ�糡������ǡ�ô�CD���е��뿪�������������������������ڼ��Ϸ���ֱֽ�������СΪB����ǿ�ų�������ǡ�ô�AB�ߵ��е��뿪����������������ӵĺ��ʱ�Ϊ��������
��ͼ��ʾ��ˮƽ���ڵ�������ABCD�ı߳�Ϊ2R������Ϊm�������Ϊ+q�����ӣ��������ƣ���AD�ߵ��е���ijһ���ٶȽ��������������������������ڼӷ�����ADƽ�С���СΪE����ǿ�糡������ǡ�ô�CD���е��뿪�������������������������ڼ��Ϸ���ֱֽ�������СΪB����ǿ�ų�������ǡ�ô�AB�ߵ��е��뿪����������������ӵĺ��ʱ�Ϊ��������| A�� | $\frac{E}{2{B}^{2}R}$ | B�� | $\frac{B}{{E}^{2}R}$ | C�� | $\frac{E}{{B}^{2}R}$ | D�� | $\frac{B}{2{E}^{2}R}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ�����ǰ뾶Ϊr��$\frac{1}{4}$Բ���εĹ⻬�Ҿ�Ե�Ĺ����λ����ֱƽ���ڣ����¶���ˮƽ��Ե���ƽ�����ӣ��������������ˮƽ�������ǿ�糡�У��糡ǿ��ΪE������һ����Ϊm��������q��С���飨�����С������Ϊ�ʵ㣩����C���ɾ�ֹ�ͷţ�����ˮƽ����ϵ�A��ʱ�ٶȼ�Ϊ�㣬����֪������ˮƽ�����Ķ�Ħ������Ϊ�̣��������ٶ�Ϊg��������Ħ������ɵĵ�����ʧ��
��ͼ��ʾ�����ǰ뾶Ϊr��$\frac{1}{4}$Բ���εĹ⻬�Ҿ�Ե�Ĺ����λ����ֱƽ���ڣ����¶���ˮƽ��Ե���ƽ�����ӣ��������������ˮƽ�������ǿ�糡�У��糡ǿ��ΪE������һ����Ϊm��������q��С���飨�����С������Ϊ�ʵ㣩����C���ɾ�ֹ�ͷţ�����ˮƽ����ϵ�A��ʱ�ٶȼ�Ϊ�㣬����֪������ˮƽ�����Ķ�Ħ������Ϊ�̣��������ٶ�Ϊg��������Ħ������ɵĵ�����ʧ���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ���⻬��Եǽ����O����Ϸ���һ�������������С��A��O�������O����ͬһˮƽ��������һ��ͬ�ֵ�ɵ�С��B����B������Ϊq1ʱ��Aǡ�ô��ھ�ֹ����ʱA��B����������ֱ����ļнǦ�1=30�㣬��֤С��B��O����ͬһˮƽ����������O����벻�䣬��B�Ĵ�����Ϊq2ʱ��A��B����������ֱ����ļнǦ�2=60�㣬��$\frac{{q}_{1}}{{q}_{2}}$Ϊ��������
��ͼ��ʾ���⻬��Եǽ����O����Ϸ���һ�������������С��A��O�������O����ͬһˮƽ��������һ��ͬ�ֵ�ɵ�С��B����B������Ϊq1ʱ��Aǡ�ô��ھ�ֹ����ʱA��B����������ֱ����ļнǦ�1=30�㣬��֤С��B��O����ͬһˮƽ����������O����벻�䣬��B�Ĵ�����Ϊq2ʱ��A��B����������ֱ����ļнǦ�2=60�㣬��$\frac{{q}_{1}}{{q}_{2}}$Ϊ��������| A�� | $\sqrt{3}$ | B�� | $\frac{\sqrt{3}}{3}$ | C�� | 3$\sqrt{3}$ | D�� | $\frac{\sqrt{3}}{9}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ��һ�����費�Ƶĵ����ab���ڵ��費�Ƶ��㹻���ĵ����ϣ�������ΪL�������ǽӴ����ã�����⻬��������ˮƽ���ļн�Ϊ�ȣ������ϱ߽�һ����ֵΪR�ĵ��裬һ�Ÿ�ǿ��ΪB����ǿ�ų���ֱ����������ϣ�ab������Ϊm���������ٶ�Ϊg���ֽ�ab���ɾ�ֹ�ͷţ���
��ͼ��ʾ��һ�����費�Ƶĵ����ab���ڵ��費�Ƶ��㹻���ĵ����ϣ�������ΪL�������ǽӴ����ã�����⻬��������ˮƽ���ļн�Ϊ�ȣ������ϱ߽�һ����ֵΪR�ĵ��裬һ�Ÿ�ǿ��ΪB����ǿ�ų���ֱ����������ϣ�ab������Ϊm���������ٶ�Ϊg���ֽ�ab���ɾ�ֹ�ͷţ����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ͼ��ʾ���ס��ҡ������������������ת����ˮƽ�ֲ�Բ̨�ϣ�������Ϊ2m���ҡ�����������Ϊm���ס�������ΪR��������Ϊ2R����Բ̨��תʱ����ס��ҡ���ʼ����Բ̨������Ծ�ֹ����������
��ͼ��ʾ���ס��ҡ������������������ת����ˮƽ�ֲ�Բ̨�ϣ�������Ϊ2m���ҡ�����������Ϊm���ס�������ΪR��������Ϊ2R����Բ̨��תʱ����ס��ҡ���ʼ����Բ̨������Ծ�ֹ����������| A�� | ����������ٶȱȱ���������ٶ�С | |
| B�� | ������Ľ��ٶȱȱ�����Ľ��ٶ�С | |
| C�� | ����������ļ��ٶȱ�����������ļ��ٶȴ� | |
| D�� | �������ܵ����������ȱ������ܵ���������С |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com