
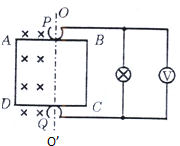
 ��ͼ��ʾ����������������ȦABCD��һ�������ǿ�ų��У��ų��ĴŸ�Ӧǿ��B=1T�������Ա߽�OO��Ϊ���Խ��ٶȦ�=100rad/s����ת������AB��CD�ߵ��е��õ��ཫ��������С���ݣ���Ȧ�߳�L=0.2m���ܵ���r=4�������ݵ���R=2��������P��Q�Ӵ����輰���ߵ��裬��
��ͼ��ʾ����������������ȦABCD��һ�������ǿ�ų��У��ų��ĴŸ�Ӧǿ��B=1T�������Ա߽�OO��Ϊ���Խ��ٶȦ�=100rad/s����ת������AB��CD�ߵ��е��õ��ཫ��������С���ݣ���Ȧ�߳�L=0.2m���ܵ���r=4�������ݵ���R=2��������P��Q�Ӵ����輰���ߵ��裬������ ��1����Em=$\frac{1}{2}$BL2�ؼ���������ֵ���������ֵ����Чֵ֮���ϵ����·�з�ѹ�ص�����ѹ��ʾ����
��2������$\overline{E}$=$\frac{n��∅}{��t}$���ƽ���綯�ƣ�
��3��������Чֵ�ͽ����������������
��4���ٸ���$q=\frac{��∅}{{R}_{��}}$��������⣮
��� �⣺��1����Em=$\frac{1}{2}$BL2�ؽ�綯�Ƶ����ֵΪ��Em=$\frac{1}{2}$��1��0.22��100V=2V��
��ЧֵΪ��E=$\frac{{E}_{m}}{\sqrt{2}}$=$\sqrt{2}$V��
���ݷ�ѹ�ص�õ�ѹ������Ϊ��U=$\frac{\frac{2��2}{2+2}}{2+\frac{2��2}{2+2}}$��$\sqrt{2}$=$\frac{\sqrt{2}}{3}$V��
��2�����ݷ����ڵ�Ÿ�Ӧ���ɵô�ͼʾλ�ÿ�ʼ������Ȧת��90��Ĺ����У�
��Ȧ�в�����ƽ����Ӧ����Ϊ$\overline{E}$=$\frac{n��∅}{��t}$=$\frac{\frac{B{L}^{2}}{2}}{\frac{T}{4}}$=$\frac{2B{L}^{2}}{\frac{2��}{��}}$=$\frac{1��0��{2}^{2}��100}{��}$V=$\frac{4}{��}$V��
��3�����ݽ������ɵô�ͼʾλ�ÿ�ʼ������Ȧת��90��Ĺ����У������ϲ���������ΪQ=I2Rt=��$\frac{\frac{\sqrt{2}}{3}}{2}$��2��2��$\frac{��}{2��100}$=$\frac{��}{600}$J��
��4����ͼʾλ�ÿ�ʼ������Ȧת��Ȧ180��Ĺ����У�������Ȧ�Ĵ�ͨ���ı仯��Ϊ��∅=BL2
ͨ�����ݵIJ����ĵ�ɵ����q��=$\frac{q}{2}$=$\frac{1}{2}��\frac{B{L}^{2}}{R+\frac{R}{2}}$=$\frac{1}{150}$C��
�𣺣�1�������ѹ���Ķ���$\frac{\sqrt{2}}{3}$V��
��2����ͼʾλ�ÿ�ʼ������Ȧת��90��Ĺ����в�����ƽ����Ӧ�綯��Ϊ$\frac{4}{��}$V��
��3����ͼʾλ�ÿ�ʼ������Ȧת��Ȧ90��Ĺ����е����ϲ�����������$\frac{��}{600}$J��
��4����ͼʾλ�ÿ�ʼ������Ȧת��Ȧ180��Ĺ����У�ͨ�����ݵIJ����ĵ������$\frac{1}{150}$C��
���� ���������Ҫ֪��������ķ�ֵ����Чֵ֮��Ĺ�ϵ������֪����·�Ĵ�������ϵ����Ҫ�ر�ע����Ч�������Ȧ�����һ�룬���������������ۺϱ���ʽ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��

| A�� | ����Ϊ5s�����Ϊ10cm | |
| B�� | 2sĩ�ʵ���ٶ�Ϊ�� | |
| C�� | 3sĩ�ʵ���ٶ�Ϊ���ֵ��������С | |
| D�� | 2s-3s���ʱ���ڣ��ظ�����������3s-4s���ʱ�������������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ���嶯��һ�������仯 | B�� | ������һ��������ʩ�ӳ��� | ||
| C�� | ���嶯��һ�������仯 | D�� | ������һ������������ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | 0.4km/s | B�� | 1.8km/s | C�� | 11km/s | D�� | 36km/s |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
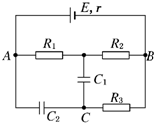 ��ͼ��ʾ����Դ�綯��E=12V������r=1��������R1=3����R2=2����R3=5�����������ĵ���C1=4 ��F��C2=1 ��F����C1��C2�����������
��ͼ��ʾ����Դ�綯��E=12V������r=1��������R1=3����R2=2����R3=5�����������ĵ���C1=4 ��F��C2=1 ��F����C1��C2������������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 һСľ�����Բ���ϣ�Сľ��m=1kg����ת��r=4cm��Բ��ת��=10rad/s��Сľ����Բ�̶�Ħ��������=0.3����Сľ�������Ħ�������ڻ���Ħ������Сľ���ڸô��ܷ�����Ծ�ֹ״̬���ڸô����ھ�ֹ�������Ƕ��g=10m/s2��
һСľ�����Բ���ϣ�Сľ��m=1kg����ת��r=4cm��Բ��ת��=10rad/s��Сľ����Բ�̶�Ħ��������=0.3����Сľ�������Ħ�������ڻ���Ħ������Сľ���ڸô��ܷ�����Ծ�ֹ״̬���ڸô����ھ�ֹ�������Ƕ��g=10m/s2���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{m{{v}_{0}}^{2}}{2}$+mgh | B�� | $\frac{m{{v}_{0}}^{2}}{2}$+mg��h+H�� | C�� | mgH | D�� | mg��h+H�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ͣ�ڸ�ѹ���ϵ�С��û�б����������ΪС����ͣ������Ϊ�� | |
| B�� | ������������̵Ķ�����������ĸ���������˵糡�� | |
| C�� | ����ͨ��ʵ���о��������˵�����Χ���ڴų�����ͨ�����ඨ���жϴų����� | |
| D�� | ����ѹ������ҵ�Ĺ���������������֯���в��ܲ������˿ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com