
 如图所示,直径为d的圆筒绕中心轴做匀速圆周运动,枪口发射的子弹速度为v,并沿直径匀速穿过圆筒,若子弹穿出后在圆筒上只留下一个弹孔,则圆筒运动的角速度为多少?
如图所示,直径为d的圆筒绕中心轴做匀速圆周运动,枪口发射的子弹速度为v,并沿直径匀速穿过圆筒,若子弹穿出后在圆筒上只留下一个弹孔,则圆筒运动的角速度为多少? 分析 子弹沿圆筒直径穿过圆筒,结果发现圆筒上只有一个弹孔,在子弹飞行的时间内,圆筒转动的角度为(2n-1)π,n=1、2、3…,结合角速度求出时间,从而得出子弹的速度.
解答 解:在子弹飞行的时间内,圆筒转动的角度为(2n-1)π,n=1、2、3…,
则时间:
$t=\frac{(2n-1)π}{ω}$,(n=1、2、3…).
所以子弹的速度:
$v=\frac{d}{t}$,
解得:
$ω=\frac{(2n-1)πv}{d}$,(n=1、2、3…).
答:
圆筒运动的角速度为$ω=\frac{(2n-1)πv}{d}$,(n=1、2、3…).
点评 解决本题的关键知道圆筒转动的周期性,结合转过角度的通项式得出运动的时间,抓住子弹飞行的时间和圆筒转动时间相等进行求解.


科目:高中物理 来源: 题型:选择题
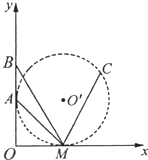 如图所示,在竖直平面内建立直角坐标系xOy,该平面内有AM、BM、CM三条光滑固定轨道,其中A、C两点处于同一个圆上,C是圆上任意一点,A、M分别为此圆与x、y轴的切点.B点在y轴上且∠BMO=60°,O′为圆心.现将a、b、c三个小球分别从A、B、C点同时由静止释放,它们将沿轨道运动到M点,如所用时间分别为tA、tB、tC,则tA、tB、tC大小关系是( )
如图所示,在竖直平面内建立直角坐标系xOy,该平面内有AM、BM、CM三条光滑固定轨道,其中A、C两点处于同一个圆上,C是圆上任意一点,A、M分别为此圆与x、y轴的切点.B点在y轴上且∠BMO=60°,O′为圆心.现将a、b、c三个小球分别从A、B、C点同时由静止释放,它们将沿轨道运动到M点,如所用时间分别为tA、tB、tC,则tA、tB、tC大小关系是( )| A. | tA<tC<tB | |
| B. | tA=tC<tB | |
| C. | tA=tC=tB | |
| D. | 由于C点的位置不确定,无法比较时间大小关系 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | $\frac{Uρt}{SL}$ | B. | $\frac{USt}{ρL}$ | C. | $\frac{Ut}{ρLS}$ | D. | $\frac{ULt}{ρS}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 质量为m的物体A静止在倾角为θ的斜面体B上,物体与斜面体间的动摩擦因数为μ,物体A始终相对于斜面体静止,求:
质量为m的物体A静止在倾角为θ的斜面体B上,物体与斜面体间的动摩擦因数为μ,物体A始终相对于斜面体静止,求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示为一种小型电风扇电路图,其中理想变压器的原、副线圈的匝数比为n:1,原线圈接电压为U的交流电源,输出端接有一只电阻为R的灯泡L和风扇电动机D,电动机线圈电阻为r.接通电源后,电风扇正常运转,测出通过风扇电动机的电流为I,则下列说法正确的是( )
如图所示为一种小型电风扇电路图,其中理想变压器的原、副线圈的匝数比为n:1,原线圈接电压为U的交流电源,输出端接有一只电阻为R的灯泡L和风扇电动机D,电动机线圈电阻为r.接通电源后,电风扇正常运转,测出通过风扇电动机的电流为I,则下列说法正确的是( )| A. | 风扇电动机D两端的电压为Ir | |
| B. | 风扇电动机D输出的机械功率为$\frac{UI}{n}$ | |
| C. | 理想变压器的输入功率为$\frac{UI}{n}$+$\frac{{U}^{2}}{{n}^{2}R}$ | |
| D. | 若电风扇由于机械故障被卡住,则通过原线圈的电流为$\frac{U(R+r)}{{n}^{2}Rr}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,在xOy平面第Ⅲ象限内的直线OM是电场与磁场的分界线,OM与负x轴成45°角.在x<0且OM的左侧空间存在着负x方向的匀强电场,场强大小E=32N/C;在y<0且OM的右侧空间存在着垂直纸面向里的匀强磁场,磁感应强度大小B=0.1T.一个不计重力的带负电的微粒,从坐标原点D沿y轴负方向以v0=2×103m/s的初速度进入磁场,最终离开电场、磁场区域.已知微粒的电荷量q=-5×10-18C,质量,m=1×10-24 kg,求:
如图所示,在xOy平面第Ⅲ象限内的直线OM是电场与磁场的分界线,OM与负x轴成45°角.在x<0且OM的左侧空间存在着负x方向的匀强电场,场强大小E=32N/C;在y<0且OM的右侧空间存在着垂直纸面向里的匀强磁场,磁感应强度大小B=0.1T.一个不计重力的带负电的微粒,从坐标原点D沿y轴负方向以v0=2×103m/s的初速度进入磁场,最终离开电场、磁场区域.已知微粒的电荷量q=-5×10-18C,质量,m=1×10-24 kg,求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题

| A. | 在水中a光的临界角比b光的临界角大 | |
| B. | 在水中a光的速度比b光的速度小 | |
| C. | 用a、b光分别做单颖衍射实验时它们的衍射条纹宽度都是均匀的 | |
| D. | 用同一双缝干涉实验装置分别以a、b光做实验,a光的干涉条纹间距小于b光的干涉条纹间距 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com