练习册

  • 练习册
  • 试题
    精英家教网 > 高中物理 > 题目详情

    如图4-7所示，两根轻绳同系一个质量m=0.1kg的小球，两绳的另一端分别固定在轴上的A、B两处，上面绳AC长L=2m，当两绳都拉直时，与轴的夹角分别为30°和45°，求当小球随轴一起在水平面内做匀速圆周运动角速度为ω=4rad/s时，上下两轻绳拉力各为多少？

       ①

          ②

    代入数据得：，

    要使BC绳有拉力，应有ω>ω1，当AC绳恰被拉直，但其拉力T1恰为零，设此时角速度为ω2，BC绳拉力为T2，则有  ③

      T2sin45°=mLACsin30°④

    代入数据得：ω2=3.16rad/s。要使AC绳有拉力，必须ω<ω2，依题意ω=4rad/s>ω2，故AC绳已无拉力，AC绳是松驰状态，BC绳与杆的夹角θ>45°，对小球有：

    T2cosθ=m ω2LBCsin θ ⑤

    而LACsin30°=LBCsin45°   LBC=m     ⑥

    由⑤、⑥可解得   ；

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中物理 来源： 题型：

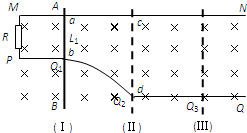    精英家教网如图所示，两根不计电阻的金属导线MN与PQ 放在水平面内，MN是直导线，PQ的PQ1段是直导线，Q1Q2段是弧形导线，Q2Q3段是直导线，MN、PQ1、Q2Q3相互平行．M、P间接入一个阻值R=0.25Ω的电阻．质量m=1.0kg、不计电阻的金属棒AB能在MN、PQ上无摩擦地滑动，金属棒始终垂直于MN，整个装置处于磁感应强度B=0.5T的匀强磁场中，磁场方向竖直向下．金属棒处于位置（I）时，给金属棒一向右的初速度v1=4 m/s，同时给一方向水平向右F1=3N的外力，使金属棒向右做匀减速直线运动；当金属棒运动到位置（Ⅱ）时，外力方向不变，改变大小，使金属棒向右做匀速直线运动2s到达位置（Ⅲ）．已知金属棒在位置（I）时，与MN、Q1Q2相接触于a、b两点，a、b的间距L1=1 m；金属棒在位置（Ⅱ）时，棒与MN、Q1Q2相接触于c、d两点；位置（I）到位置（Ⅱ）的距离为7.5m．求：
    （1）金属棒向右匀减速运动时的加速度大小；
    （2）c、d两点间的距离L2；
    （3）金属棒从位置（I）运动到位置（Ⅲ）的过程中，电阻R上放出的热量Q．

    查看答案和解析>>

    科目：高中物理 来源： 题型：

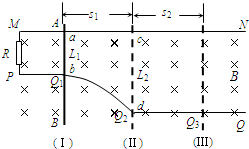    精英家教网如图所示，两根不计电阻的金属导线MN与PQ 放在水平面内，MN是直导线，PQ的PQ1段是直导线，Q1Q2段是弧形导线，Q2Q3段是直导线，MN、PQ1、Q2Q3相互平行，M、P间接入一个阻值R=0.25Ω的电阻．一根质量为1.0kg不计电阻的金属棒AB能在MN、PQ上无摩擦地滑动，金属棒始终垂直于MN，整个装置处于磁感应强度B=0.5T的匀强磁场中，磁场方向竖直向下．金属棒处于位置（I）时，给金属棒一个向右的速度v1=4 m/s，同时方向水平向右的外力F1=3N作用在金属棒上使金属棒向右做匀减速直线运动；当金属棒运动到位置（Ⅱ）时，外力方向不变，大小变为F2，金属棒向右做匀速直线运动，经过时间t=2s到达位置（Ⅲ）．金属棒在位置（I）时，与MN、Q1Q2相接触于a、b两点，a、b的间距L1=1 m，金属棒在位置（Ⅱ）时，棒与MN、Q1Q2相接触于c、d两点．已知s1=7.5m．求：
    （1）金属棒向右匀减速运动时的加速度大小？
    （2）c、d两点间的距离L2=？
    （3）外力F2的大小？
    （4）金属棒从位置（I）运动到位置（Ⅲ）的过程中，电阻R上放出的热量Q=？

    查看答案和解析>>

    科目：高中物理 来源： 题型：

    如图4-7-16所示，一个半球形的碗放在桌面上，碗口水平，O点为其球心，碗的内表面及碗口是光滑的.一根细线跨在碗口上，线的两端分别系有质量为m1和m2的小球，当它们处于平衡状态时，质量为m1的小球与O点的连线与水平线夹角为α=60°.两个球的质量比为（　　）?

     图4-7-16

    ?    A.　 ?    B.    ?    C.    ?    D.

    查看答案和解析>>

    科目：高中物理 来源： 题型：阅读理解

    第十部分 磁场

    第一讲 基本知识介绍

    《磁场》部分在奥赛考刚中的考点很少，和高考要求的区别不是很大，只是在两处有深化：a、电流的磁场引进定量计算；b、对带电粒子在复合场中的运动进行了更深入的分析。

    一、磁场与安培力

    1、磁场

    a、永磁体、电流磁场→磁现象的电本质

    b、磁感强度、磁通量

    c、稳恒电流的磁场

    *毕奥-萨伐尔定律（Biot-Savart law）：对于电流强度为I 、长度为dI的导体元段，在距离为r的点激发的“元磁感应强度”为dB 。矢量式d= k，（d表示导体元段的方向沿电流的方向、为导体元段到考查点的方向矢量）；或用大小关系式dB = k结合安培定则寻求方向亦可。其中 k = 1.0×10?7N/A2 。应用毕萨定律再结合矢量叠加原理，可以求解任何形状导线在任何位置激发的磁感强度。

    毕萨定律应用在“无限长”直导线的结论：B = 2k ；

    *毕萨定律应用在环形电流垂直中心轴线上的结论：B = 2πkI ；

    *毕萨定律应用在“无限长”螺线管内部的结论：B = 2πknI 。其中n为单位长度螺线管的匝数。

    2、安培力

    a、对直导体，矢量式为 = I；或表达为大小关系式 F = BILsinθ再结合“左手定则”解决方向问题（θ为B与L的夹角）。

    b、弯曲导体的安培力

    ⑴整体合力

    折线导体所受安培力的合力等于连接始末端连线导体（电流不变）的的安培力。

    证明：参照图9-1，令MN段导体的安培力F1与NO段导体的安培力F2的合力为F，则F的大小为

    F = 

      = BI

      = BI

    关于F的方向，由于ΔFF2P∽ΔMNO，可以证明图9-1中的两个灰色三角形相似，这也就证明了F是垂直MO的，再由于ΔPMO是等腰三角形（这个证明很容易），故F在MO上的垂足就是MO的中点了。

    证毕。

    由于连续弯曲的导体可以看成是无穷多元段直线导体的折合，所以，关于折线导体整体合力的结论也适用于弯曲导体。（说明：这个结论只适用于匀强磁场。）

    ⑵导体的内张力

    弯曲导体在平衡或加速的情形下，均会出现内张力，具体分析时，可将导体在被考查点切断，再将被切断的某一部分隔离，列平衡方程或动力学方程求解。

    c、匀强磁场对线圈的转矩

    如图9-2所示，当一个矩形线圈（线圈面积为S、通以恒定电流I）放入匀强磁场中，且磁场B的方向平行线圈平面时，线圈受安培力将转动（并自动选择垂直B的中心轴OO′，因为质心无加速度），此瞬时的力矩为

    M = BIS

    几种情形的讨论——

    ⑴增加匝数至N ，则 M = NBIS ；

    ⑵转轴平移，结论不变（证明从略）；

    ⑶线圈形状改变，结论不变（证明从略）；

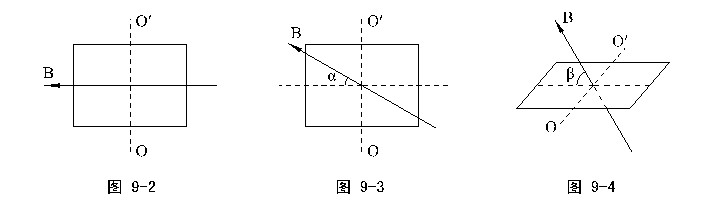
    *⑷磁场平行线圈平面相对原磁场方向旋转α角，则M = BIScosα ，如图9-3；

    证明：当α = 90°时，显然M = 0 ，而磁场是可以分解的，只有垂直转轴的的分量Bcosα才能产生力矩…

    ⑸磁场B垂直OO′轴相对线圈平面旋转β角，则M = BIScosβ ，如图9-4。

    证明：当β = 90°时，显然M = 0 ，而磁场是可以分解的，只有平行线圈平面的的分量Bcosβ才能产生力矩…

    说明：在默认的情况下，讨论线圈的转矩时，认为线圈的转轴垂直磁场。如果没有人为设定，而是让安培力自行选定转轴，这时的力矩称为力偶矩。

    二、洛仑兹力

    1、概念与规律

    a、 = q，或展开为f = qvBsinθ再结合左、右手定则确定方向（其中θ为与的夹角）。安培力是大量带电粒子所受洛仑兹力的宏观体现。

    b、能量性质

    由于总垂直与确定的平面，故总垂直 ，只能起到改变速度方向的作用。结论：洛仑兹力可对带电粒子形成冲量，却不可能做功。或：洛仑兹力可使带电粒子的动量发生改变却不能使其动能发生改变。

    问题：安培力可以做功，为什么洛仑兹力不能做功？

    解说：应该注意“安培力是大量带电粒子所受洛仑兹力的宏观体现”这句话的确切含义——“宏观体现”和“完全相等”是有区别的。我们可以分两种情形看这个问题：（1）导体静止时，所有粒子的洛仑兹力的合力等于安培力（这个证明从略）；（2）导体运动时，粒子参与的是沿导体棒的运动v1和导体运动v2的合运动，其合速度为v ，这时的洛仑兹力f垂直v而安培力垂直导体棒，它们是不可能相等的，只能说安培力是洛仑兹力的分力f1 = qv1B的合力（见图9-5）。

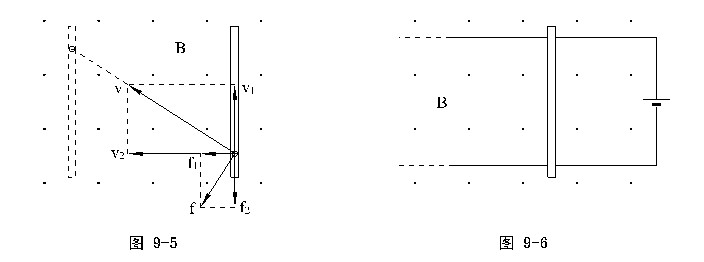
    很显然，f1的合力（安培力）做正功，而f不做功（或者说f1的正功和f2的负功的代数和为零）。（事实上，由于电子定向移动速率v1在10?5m/s数量级，而v2一般都在10?2m/s数量级以上，致使f1只是f的一个极小分量。）

    ☆如果从能量的角度看这个问题，当导体棒放在光滑的导轨上时（参看图9-6），导体棒必获得动能，这个动能是怎么转化来的呢？

    若先将导体棒卡住，回路中形成稳恒的电流，电流的功转化为回路的焦耳热。而将导体棒释放后，导体棒受安培力加速，将形成感应电动势（反电动势）。动力学分析可知，导体棒的最后稳定状态是匀速运动（感应电动势等于电源电动势，回路电流为零）。由于达到稳定速度前的回路电流是逐渐减小的，故在相同时间内发的焦耳热将比导体棒被卡住时少。所以，导体棒动能的增加是以回路焦耳热的减少为代价的。

    2、仅受洛仑兹力的带电粒子运动

    a、⊥时，匀速圆周运动，半径r =  ，周期T = 

    b、与成一般夹角θ时，做等螺距螺旋运动，半径r =  ，螺距d = 

    这个结论的证明一般是将分解…（过程从略）。

    ☆但也有一个问题，如果将分解（成垂直速度分量B2和平行速度分量B1 ，如图9-7所示），粒子的运动情形似乎就不一样了——在垂直B2的平面内做圆周运动？

    其实，在图9-7中，B1平行v只是一种暂时的现象，一旦受B2的洛仑兹力作用，v改变方向后就不再平行B1了。当B1施加了洛仑兹力后，粒子的“圆周运动”就无法达成了。（而在分解v的处理中，这种局面是不会出现的。）

    3、磁聚焦

    a、结构：见图9-8，K和G分别为阴极和控制极，A为阳极加共轴限制膜片，螺线管提供匀强磁场。

    b、原理：由于控制极和共轴膜片的存在，电子进磁场的发散角极小，即速度和磁场的夹角θ极小，各粒子做螺旋运动时可以认为螺距彼此相等（半径可以不等），故所有粒子会“聚焦”在荧光屏上的P点。

    4、回旋加速器

    a、结构&原理（注意加速时间应忽略）

    b、磁场与交变电场频率的关系

    因回旋周期T和交变电场周期T′必相等，故 =

    c、最大速度 vmax = = 2πRf

    5、质谱仪

    速度选择器&粒子圆周运动，和高考要求相同。

    第二讲 典型例题解析

    一、磁场与安培力的计算

    【例题1】两根无限长的平行直导线a、b相距40cm，通过电流的大小都是3.0A，方向相反。试求位于两根导线之间且在两导线所在平面内的、与a导线相距10cm的P点的磁感强度。

    【解说】这是一个关于毕萨定律的简单应用。解题过程从略。

    【答案】大小为8.0×10?6T ，方向在图9-9中垂直纸面向外。

    【例题2】半径为R ，通有电流I的圆形线圈，放在磁感强度大小为B 、方向垂直线圈平面的匀强磁场中，求由于安培力而引起的线圈内张力。

    【解说】本题有两种解法。

    方法一：隔离一小段弧，对应圆心角θ ，则弧长L = θR 。因为θ →

    查看答案和解析>>

    同步练习册答案