
| A. | $\frac{\sqrt{2}v}{2}$ | B. | $\frac{v}{2}$ | C. | $\frac{v}{4}$ | D. | $\sqrt{2}$v |
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中物理 来源: 题型:选择题
| A. | 日心说的代表人物是托勒密 | |
| B. | 开普勒提出行星运动规律,并发现了万有引力定律 | |
| C. | 牛顿发现太阳与行星间引力的过程中,得出太阳对行星的引力表达式后推出行星对太阳的引力表达式,这是一个很关键的论证步骤,这一步骤采用的论证方法是类比法 | |
| D. | 牛顿发现了万有引力定律并通过精确的计算得出万有引力常量 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
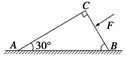 如图所示,顶角为直角、质量为M的斜面体ABC放在粗糙的水平面上,∠A=30°,斜面体与水平面间的动摩擦因数为μ.现沿垂直于BC方向对斜面体施加力F,斜面体仍保持静止状态,求:
如图所示,顶角为直角、质量为M的斜面体ABC放在粗糙的水平面上,∠A=30°,斜面体与水平面间的动摩擦因数为μ.现沿垂直于BC方向对斜面体施加力F,斜面体仍保持静止状态,求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,粗糙程度均匀的绝缘斜面下方O处有一正点电荷,带负电的小物体以初速度v1从M点沿斜面上滑,到达N点时速度为零,然后下滑回到M点,此时速度为v2(v2<v1).若小物体电荷量保持不变,OM=ON,则( )
如图所示,粗糙程度均匀的绝缘斜面下方O处有一正点电荷,带负电的小物体以初速度v1从M点沿斜面上滑,到达N点时速度为零,然后下滑回到M点,此时速度为v2(v2<v1).若小物体电荷量保持不变,OM=ON,则( )| A. | 小物体上升的最大高度为$\frac{{v}_{1}^{2}{+v}_{2}^{2}}{4g}$ | |
| B. | 全程小物体克服摩擦力做的功为$\frac{1}{2}$mv12-$\frac{1}{2}$mv22 | |
| C. | 从M到N点的过程中,电场力对小物体先做负功后做正功 | |
| D. | 从N点到M点的过程中,小物体受到的摩擦力和电场力均是先增大后减小 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
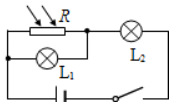 如图所示电路中,L1、L2为两只完全相同、阻值恒定的灯泡,R为光敏电阻(光照越强,阻值越小).闭合电键S后,随着光照强度逐渐增强( )
如图所示电路中,L1、L2为两只完全相同、阻值恒定的灯泡,R为光敏电阻(光照越强,阻值越小).闭合电键S后,随着光照强度逐渐增强( )| A. | L1逐渐变暗,L2逐渐变亮 | |
| B. | L1逐渐变亮,L2逐渐变暗 | |
| C. | 电源内电路消耗的功率逐渐减小 | |
| D. | 光敏电阻R和灯泡L1消耗的总功率逐渐增大 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 在图所示的电路中,电源电压U=15V,电阻R1、R2、R3的阻值均为10Ω,S为单刀三掷电键,当电键S分别接A,接B,接C时,电压表的读数正确的是( )
在图所示的电路中,电源电压U=15V,电阻R1、R2、R3的阻值均为10Ω,S为单刀三掷电键,当电键S分别接A,接B,接C时,电压表的读数正确的是( )| A. | 0V 7.5V10V | B. | 0V 10V 7.5V | ||
| C. | 7.5V 0V 10V | D. | 7.5V 10V 0V |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
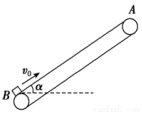 如图,倾角为α的传送带AB以速度v逆时针匀速转动.质量为m的小物块与传送带间的动摩擦因数μ<tan α.小物块以沿传送带向上的初速度v0从传送带上的B位置开始运动,则传送带对物块的摩擦力做功的最大功率是( )
如图,倾角为α的传送带AB以速度v逆时针匀速转动.质量为m的小物块与传送带间的动摩擦因数μ<tan α.小物块以沿传送带向上的初速度v0从传送带上的B位置开始运动,则传送带对物块的摩擦力做功的最大功率是( )| A. | μmg$\sqrt{{{v}_{0}}^{2}+{v}^{2}}$cos α | B. | μmgvcos α | ||
| C. | μmgv0cos α | D. | $\frac{1}{2}$μmg(v0+v)cos α |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com