
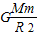 =
=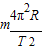
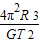
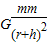 =
=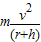
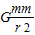 =mg
=mg 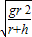
 ;
;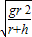 .
.

科目:高中物理 来源:物理教研室 题型:038
查看答案和解析>>
科目:高中物理 来源: 题型:038
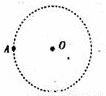
宇宙中有一种双星,质量分别为m1、m2的两颗星球,如图所示,绕同一圆心做匀速圆周运动,它们之间的距离恒为L,不考虑其他星体影响,两颗星的轨道半径和周期各是多少?
查看答案和解析>>
科目:高中物理 来源: 题型:
宇宙中存在一些离其它恒星很远的四颗恒星组成的四星系统,通常可忽略其它星体对它们的引力作用。稳定的四星系统存在多种形式,其中一种是四颗质量相等的恒星位于正方形的四个顶点上,沿着外接于正方形的圆形轨道做匀速圆周运行;另一种如图所示,四颗恒星始终位于同一直线上,均围绕中点O 做匀速圆周运动。已知万有引力常最为G,请回答:
(1)已知第一种形式中的每颗恒星质量均为m,正方形边长为L,求其中一颗恒星受到的合力;
(2)已知第二种形式中的两外侧恒星质量均为m、两内侧恒星质最均为M ,四颗恒星始终位于同一直线,且相邻恒星之间距离相等,求内侧恒星质量M与外侧恒质m的比值 。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com