
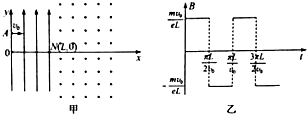
分析 (1)电子在匀强电场中做类平抛运动,应用类平抛运动的规律可以求出电子的速度.
(2)电子在磁场中做匀速圆周运动,洛伦兹力提供向心力,应用牛顿第二定律求出磁感应强度.
(3)根据电子做圆周运动的周期求出粒子与电子相碰撞的时间,粒子做匀速直线运动,应用速度公式可以求出粒子P的速度.
解答 解:(1)电子在电场中做类平抛运动,
水平方向:L=v0t1,
竖直方向:vy=at1=$\frac{eE}{m}$t1,
电子离开电场时的速度:v=$\sqrt{{v}_{0}^{2}+{v}_{y}^{2}}$,
解得:v=$\sqrt{2}$v0,
速度与x轴方向夹角θ,tanθ=$\frac{{v}_{y}}{{v}_{0}}$,
解得:θ=45°;
(2)电子在电场中竖直方向的位移:y=$\frac{1}{2}$at12=$\frac{1}{2}$$\frac{eE}{m}$t12=$\frac{L}{2}$,
电子从N点进入磁场,电子不能进入x>2L的区域,由几何关系可知:Rsinθ+R≤L,
电子在磁场中做匀速圆周运动,洛伦兹力提供向心力,
由牛顿第二定律得:evB=m$\frac{{v}^{2}}{R}$,
解得:B≥$\frac{(\sqrt{2}+1)m{v}_{0}}{eL}$;
(3)电子在磁场中做匀速圆周运动的周期:T=$\frac{2πm}{e{B}_{0}}$=$\frac{2πL}{{v}_{0}}$,
电子运动轨迹如图所示,电子轨道半径:r=$\frac{\sqrt{2}m{v}_{0}}{e{B}_{0}}$=$\sqrt{2}$L,
电子经过x轴的时间:t2=n$\frac{T}{4}$=$\frac{nπL}{2{v}_{0}}$ (n=1、2、3…)
粒子P与电阻相碰时的位移:x=$\sqrt{2}$nr (n=1、2、3…),
两粒子相碰的时间:t=t1+t2,
粒子P的速度:vP=$\frac{x}{t}$,
解得:vP=$\frac{4n{v}_{0}}{2+nπ}$ (n=1、2、3…);
答:(1)电子进入磁场区域时速度v的大小为$\sqrt{2}$v0,与x轴方向夹45°角;
(2)若使电子不能进入x>2L的区域,磁感应强度的大小为B≥$\frac{(\sqrt{2}+1)m{v}_{0}}{eL}$;
(3)粒子P的速度为$\frac{4n{v}_{0}}{2+nπ}$ (n=1、2、3…).
点评 本题考查了粒子在电场与磁场中的运动,带电粒子在复合场中的运动,分别采用不同的处理方法;电子在电场中,关键是将粒子的运动沿着水平方向和竖直方向正交分解,然后根据牛顿运动定律和运动学公式列式分析求解;在磁场中,关键要画出轨迹图分析,根据几何关系与牛顿第二定律求解.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中物理 来源: 题型:解答题
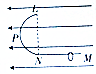 如图所示,在E=75V/m的水平方向的匀强电场中,有一光滑的半圆形绝缘轨道LPN与一水平绝缘轨道MN连接,半圆形所在的竖直平面与电场线平行,其半径R=0.40m.其中P为LN圆弧的中点,直径LN与水平轨道MN垂直,另有一个带正电荷量q=1×10-3C,质量m=1.0×10-2kg的小环套在轨道上,此环自位于N点右侧x=1.2m处以初速度v0向左开始运动,已知小环与水平轨道间的动摩擦因数μ=0.25,且它恰能运动到圆轨道的最高点L,取g=10m/s2 ,求:
如图所示,在E=75V/m的水平方向的匀强电场中,有一光滑的半圆形绝缘轨道LPN与一水平绝缘轨道MN连接,半圆形所在的竖直平面与电场线平行,其半径R=0.40m.其中P为LN圆弧的中点,直径LN与水平轨道MN垂直,另有一个带正电荷量q=1×10-3C,质量m=1.0×10-2kg的小环套在轨道上,此环自位于N点右侧x=1.2m处以初速度v0向左开始运动,已知小环与水平轨道间的动摩擦因数μ=0.25,且它恰能运动到圆轨道的最高点L,取g=10m/s2 ,求:查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图,在场强大小为E、水平向右的匀强电场中,一轻杆可绕固定转轴O在竖直平面内自由转动.杆的两端分别固定两电荷量均为q的小球A、B,A带正电,B带负电;A、B两球到转轴O的距离分别为2l、l,所受重力大小均为电场力大小的$\sqrt{3}$倍.开始时杆与电场间夹角为θ(90°≤θ≤180°).将杆从初始位置由静止释放,以O点为重力势能和电势能零点.求:
如图,在场强大小为E、水平向右的匀强电场中,一轻杆可绕固定转轴O在竖直平面内自由转动.杆的两端分别固定两电荷量均为q的小球A、B,A带正电,B带负电;A、B两球到转轴O的距离分别为2l、l,所受重力大小均为电场力大小的$\sqrt{3}$倍.开始时杆与电场间夹角为θ(90°≤θ≤180°).将杆从初始位置由静止释放,以O点为重力势能和电势能零点.求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
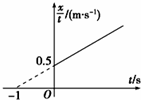 一个物体沿直线运动,从t=0时刻开始,物体的$\frac{x}{t}$-t的图象如图所示,图线与横、纵坐标轴的交点分别为-1s和0.5m/s,由此可知( )
一个物体沿直线运动,从t=0时刻开始,物体的$\frac{x}{t}$-t的图象如图所示,图线与横、纵坐标轴的交点分别为-1s和0.5m/s,由此可知( )| A. | 物体做速度大小为0.5 m/s的匀速直线运动 | |
| B. | 物体做变加速直线运动 | |
| C. | 物体做匀加速运动,加速度的大小为0.5 m/s2 | |
| D. | 物体做匀加速运动,初速度大小为0.5 m/s |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
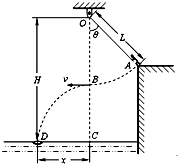 某水上游乐场举办了一场趣味水上比赛.如图所示,质量m=50kg的参赛者(可视为质点),在河岸上A点紧握一根长L=5.0m的不可伸长的轻绳,轻绳另一端系在距离水面高H=10.0m的O点,此时轻绳与竖直方向的夹角为θ=37°,C点是位于O点正下方水面上的一点,距离C点x=4.8m处的D点固定着一只救生圈,O、A、C、D各点均在同一竖直面内.若参赛者抓紧绳端点,从台阶上A点沿垂直于轻绳斜向下以一定的初速度跃出,当摆到O点正下方的B点时松开手,此后恰能落在救生圈内.(sin37°=0.6,cos37°=0.8,$\sqrt{12.96}$=3.6,g=10m/s2)
某水上游乐场举办了一场趣味水上比赛.如图所示,质量m=50kg的参赛者(可视为质点),在河岸上A点紧握一根长L=5.0m的不可伸长的轻绳,轻绳另一端系在距离水面高H=10.0m的O点,此时轻绳与竖直方向的夹角为θ=37°,C点是位于O点正下方水面上的一点,距离C点x=4.8m处的D点固定着一只救生圈,O、A、C、D各点均在同一竖直面内.若参赛者抓紧绳端点,从台阶上A点沿垂直于轻绳斜向下以一定的初速度跃出,当摆到O点正下方的B点时松开手,此后恰能落在救生圈内.(sin37°=0.6,cos37°=0.8,$\sqrt{12.96}$=3.6,g=10m/s2)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com