
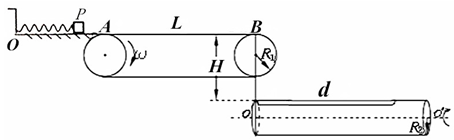
分析 (1)小滑块P恰好到达B点时,弹簧的弹性势能Ep全部克服摩擦力做功,利用能量守恒,即可求出弹簧弹性势能Ep的最小值;
(2)滑块离开B后做平抛运动,恰好落入圆桶的小孔内,找出下落时间与圆筒初始位置以及圆筒周期之间的关系,即可求出圆筒周期.
(3)滑块离开B后做平抛运动,要恰好落入圆桶的小孔内并穿过,水平位移大小大于s,根据平抛运动的规律求得滑块经过C点的最小速度;同理求出小球再次穿过的时间与水平速度,从而确定传送带的速度的范围,然后由v=ωr求出传送带转动轮的角速度ω.
解答 解:(1)由功能关系可知:Ep=μmgL
解得:Ep=11J
(2)从B点飞出到圆筒上端:$H=\frac{1}{2}g{t_1}^2$
因为P飞离传送带时,长槽恰好转动到圆筒的正下方,
根据圆筒匀速转动周期性可知:${t_1}=\frac{T}{2}+nT$ (n=0,1,2,3…)
解得:$T=\frac{1}{2n+1}$s(n=0,1,2,3…)
(3)小滑块P能从B点飞离需满足:$mg≤m\frac{{{v_1}^2}}{R_1}$,
得到:v1≥2m/s
设小滑块P从C点下落到下端位置的时间t2:$H+2{R_2}=\frac{1}{2}g{t_2}^2$
则小球能从长槽顺利穿出需满足条件:v2t2≤d即v2≤6 m/s
假设小滑块P在AB上全程匀减速有:${v_{min}}^2-{v_0}^2=-2μgL$
假设小滑块P在AB上全程匀加速有:${v_{max}}^2-{v_0}^2=2μgL$
解得:${v_{min}}=\sqrt{5}$m/s,vmax=7m/s
分析可知全程匀减速的末速度:${v_{min}}=\sqrt{5}m/s>2m/s$,
所以转动轮的角速度最小值为0
全程匀加速的末速度:vmax=7m/s>6m/s,
所以转动轮的角速度最大值为:$ω=\frac{v_2}{R_1}=\frac{6}{0.4}=15$ rad/s
综上分析可得:0≤ω≤15 rad/s
答:(1)若传送带保持静止,为使得P能到达B点,弹簧弹性势能至少为11J;
(2)若P能从B点飞离传送带,飞离时长槽恰好转动到圆筒的正下方,且P能进入长槽,圆筒周期为$\frac{1}{2n+1}$s(n=0,1,2,3…);
(3)传送带转动轮的角速度ω应满足0≤ω≤15 rad/s.
点评 本题考查动能定理、牛顿第二定律和运动学规律的综合运用,滑块经历三个运动过程,分段选择物理规律进行研究,关键是抓住圆盘与滑块运动的同时性,根据周期性求解ω应满足的条件,第三问要找到物块平抛水平距离最远和最近的临界条件,即:滑块恰好在传送带上一直加速,正好在最右端加速到与传送带共速时,平抛的水平位移最大;滑块恰好在传送带上一直减速,正好在最右端减速到与传送带共速时,时平抛的水平位移最小.


科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
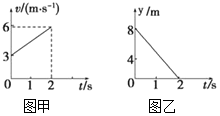 有一个质量为3kg的质点在直角坐标系xOy所在的平面内运动,x方向的速度-时间图象和y方向的位移-时间图象分别如图甲、乙所示,下列说法正确的是( )
有一个质量为3kg的质点在直角坐标系xOy所在的平面内运动,x方向的速度-时间图象和y方向的位移-时间图象分别如图甲、乙所示,下列说法正确的是( )| A. | 质点做匀加速直线运动 | |
| B. | 质点在2s内的位移大小为8m | |
| C. | 质点的初速度大小为5m/s | |
| D. | 质点初速度的方向与合外力的方向垂直 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
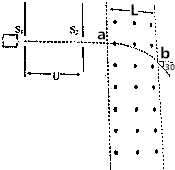 如图所示,小孔S1、S2与a在同一直线上且垂直于磁场边界,现有一个质量为m、电荷量为q的粒子,从小孔S1无初速度的进入加速电场,加速后经a点垂直磁场方向射入磁感应强度为B的有界匀强磁场中,从磁场边界b点射出,其速度方向与入射方向成θ=30°角,已知磁场宽度为L,不计粒子重力.求:
如图所示,小孔S1、S2与a在同一直线上且垂直于磁场边界,现有一个质量为m、电荷量为q的粒子,从小孔S1无初速度的进入加速电场,加速后经a点垂直磁场方向射入磁感应强度为B的有界匀强磁场中,从磁场边界b点射出,其速度方向与入射方向成θ=30°角,已知磁场宽度为L,不计粒子重力.求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 图甲是学生常使用的修正带,其原理如图乙所示,修正带跨过端口与两齿轮相连,A、B为齿轮边缘上的两点,两齿轮的半径分别为r1、r2.假设在使用修正带时,两齿轮做匀速转动,则A、B两点的( )
图甲是学生常使用的修正带,其原理如图乙所示,修正带跨过端口与两齿轮相连,A、B为齿轮边缘上的两点,两齿轮的半径分别为r1、r2.假设在使用修正带时,两齿轮做匀速转动,则A、B两点的( )| A. | 线速度之比为r1:r2 | B. | 角速度之比为r1:r2 | ||
| C. | 周期之比为r1:r2 | D. | 向心加速度之比为r1:r2 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 92235U的裂变方程为92235U→56144Ba+3689Kr+01n | |
| B. | 92235U的裂变方程为92235U+01n→56144Ba+3689Kr+301n | |
| C. | 一个92235U裂变时,质量亏损约为7.1×10-28kg | |
| D. | 一个92235U裂变时,质量亏损约为3.6×10-28kg |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 当分子间的距离变小时,分子间作用力可能减小,也可能增大 | |
| B. | 压缩理想气体时需用力,说明理想气体分子间有斥力 | |
| C. | 相同质量、相同温度的氧气和氦气的分子平均动能一定相等 | |
| D. | 液体表面层分子分布比液体内部稀疏,分子间相互作用表现为引力 | |
| E. | 一定质量的气体,当体积减小、温度升高时,压强可能减小 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 0.1m/s2 | B. | 5m/s2 | C. | 10m/s2 | D. | 20m/s2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com