
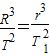
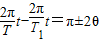
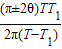 .
.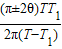 再次出现观测行星的最佳时期.
再次出现观测行星的最佳时期.

 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中物理 来源: 题型:
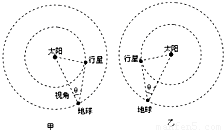
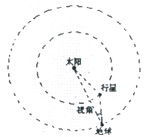 如图所示.地球和某行星在同一轨道平面内同向绕太阳做匀速圆周运动.地球的轨道半径为R,运转周期为T.地球和太阳中心的连线与地球和行星的连线所夹的角叫地球对该行星的观察视角(简称视角).已知该行星的最大视角为θ,当 行星处于最大视角处时,是地球上的天文爱好者观察该行星的最佳时期.若某时刻该行星正处于最佳观察期,问该行星下一次处于最佳观察期至少需经历多长时间?
如图所示.地球和某行星在同一轨道平面内同向绕太阳做匀速圆周运动.地球的轨道半径为R,运转周期为T.地球和太阳中心的连线与地球和行星的连线所夹的角叫地球对该行星的观察视角(简称视角).已知该行星的最大视角为θ,当 行星处于最大视角处时,是地球上的天文爱好者观察该行星的最佳时期.若某时刻该行星正处于最佳观察期,问该行星下一次处于最佳观察期至少需经历多长时间?查看答案和解析>>
科目:高中物理 来源: 题型:
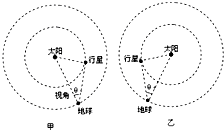 地球和某行星在同一轨道平面内同向绕太阳做匀速圆周运动.地球的轨道半径为R=1.50×1011m,运转周期为T=3.16×107s.地球和太阳中心的连线与地球和行星的连线所夹的角叫地球对该行星的观察视角(简称视角).当行星处于最大视角处时,是地球上的天文爱好者观察该行星的最佳时期,如图甲或图乙所示,该行星的最大视角θ=14.5°.求:
地球和某行星在同一轨道平面内同向绕太阳做匀速圆周运动.地球的轨道半径为R=1.50×1011m,运转周期为T=3.16×107s.地球和太阳中心的连线与地球和行星的连线所夹的角叫地球对该行星的观察视角(简称视角).当行星处于最大视角处时,是地球上的天文爱好者观察该行星的最佳时期,如图甲或图乙所示,该行星的最大视角θ=14.5°.求:查看答案和解析>>
科目:高中物理 来源: 题型:
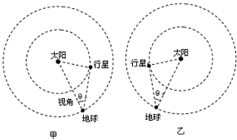 (2009?东莞模拟)地球和某行星在同一轨道平面内同向绕太阳做匀速圆周运动.地球的轨道半径为r=1.50×1011m,运转周期为T=3.16×107s.地球和太阳中心的连线与地球和行星的连线所夹的角叫地球对该行星的观察视角(简称视角),如图甲或图乙所示.当行星处于最大视角处时,是地球上的天文爱好者观察该行星的最佳时期.已知某行星的最大视角为14.5°.求该行星的轨道半径和运转周期.(sin14.5°=0.25,最终计算结果保留两位有效数字)
(2009?东莞模拟)地球和某行星在同一轨道平面内同向绕太阳做匀速圆周运动.地球的轨道半径为r=1.50×1011m,运转周期为T=3.16×107s.地球和太阳中心的连线与地球和行星的连线所夹的角叫地球对该行星的观察视角(简称视角),如图甲或图乙所示.当行星处于最大视角处时,是地球上的天文爱好者观察该行星的最佳时期.已知某行星的最大视角为14.5°.求该行星的轨道半径和运转周期.(sin14.5°=0.25,最终计算结果保留两位有效数字)查看答案和解析>>
科目:高中物理 来源: 题型:
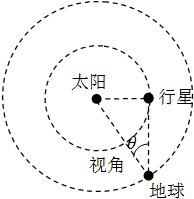 地球和某行星在同一轨道平面内同向绕太阳做匀速圆周运动.地球的轨道半径为R,运转周期为T.地球和太阳中心的连线与地球和行星的连线所夹的角叫地球对该行星的观察视角(简称视角).当行星处于最大视角处时,是地球上的天文爱好者观察该行星的最佳时期.该行星的最大视角为θ,如图所示.求该行星的轨道半径和运转周期.
地球和某行星在同一轨道平面内同向绕太阳做匀速圆周运动.地球的轨道半径为R,运转周期为T.地球和太阳中心的连线与地球和行星的连线所夹的角叫地球对该行星的观察视角(简称视角).当行星处于最大视角处时,是地球上的天文爱好者观察该行星的最佳时期.该行星的最大视角为θ,如图所示.求该行星的轨道半径和运转周期.查看答案和解析>>
科目:高中物理 来源:2010年黑龙江省高三上学期10月月考物理试题 题型:综合题
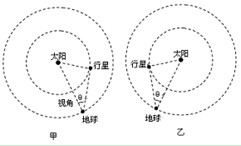
地球和某行星在同一轨道平面内同向绕太阳做匀速圆周运动。地球的轨道半径为r=1.50×1011m,运转周期为T=3.16×107s。地球和太阳中心的连线与地球和行星的连线所夹的角叫地球对该行星的观察视角(简称视角),如图甲或图乙所示。当行星处于最大视角处时,是地球上的天文爱好者观察该行星的最佳时期。已知某行星的最大视角为14.5°.求该行星的轨道半径和运转周期.(sin14.5°=0.25,最终计算结果保留两位有效数字)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com