
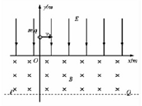
 如图所示,在直角坐标系的第一、二象限中存在沿y轴负方向的匀强电场,电场强度大小为E,在第三、四象限中存在着宽度未知的垂直纸面向里的匀强磁场,磁感应强度大小为B,x轴是其上边界,下边界与x轴平行的虚线PQ,一质量为m,带电量为+q的粒子(不计重力),从y轴上(0,y0)位置以初速度v0沿x轴正方向射入匀强电场.
如图所示,在直角坐标系的第一、二象限中存在沿y轴负方向的匀强电场,电场强度大小为E,在第三、四象限中存在着宽度未知的垂直纸面向里的匀强磁场,磁感应强度大小为B,x轴是其上边界,下边界与x轴平行的虚线PQ,一质量为m,带电量为+q的粒子(不计重力),从y轴上(0,y0)位置以初速度v0沿x轴正方向射入匀强电场.分析 (1)通过电场力做功,由动能定理求解;
(2)求得粒子进入磁场的速度大小及方向,由左手定则及几何关系求得边界宽度与半径的关系;再由洛伦兹力作向心力即可求得半径,进而求得宽度.
解答 解:(1)粒子在电场中做类平抛运动,只有电场力作用功;
设粒子第一次进入磁场时速度大小为v,则由动能定理可得$qE{y}_{0}=\frac{1}{2}m{v}^{2}-\frac{1}{2}m{{v}_{0}}^{2}$;
所以,$v=\sqrt{\frac{2qE{y}_{0}}{m}+{{v}_{0}}^{2}}$;
(2)粒子在磁场中做圆周运动,洛伦兹力作向心力,所以有$Bvq=\frac{m{v}^{2}}{R}$,所以,$R=\frac{mv}{Bq}=\frac{m}{Bq}\sqrt{\frac{2qE{y}_{0}}{m}+{{v}_{0}}^{2}}$;
设v与x轴正方向成α角,则$cosα=\frac{{v}_{0}}{v}$,如图所示, ,
,
则粒子运动在磁场中纵向位移最大为$d=R-Rcosα=R×\frac{v-{v}_{0}}{v}=\frac{m}{Bq}(\sqrt{\frac{2qE{y}_{0}}{m}+{{v}_{0}}^{2}}-{v}_{0})$=$\frac{m}{Bq}•\frac{2qE{y}_{0}}{m}\frac{1}{\sqrt{\frac{2qE{y}_{0}}{m}+{{v}_{0}}^{2}}+{v}_{0}}$;
当v0=0时,d有最大值,即$d=\frac{m}{Bq}•\sqrt{\frac{2qE{y}_{0}}{m}}=\frac{1}{B}\sqrt{\frac{2mE{y}_{0}}{q}}$;
所以,磁场的最小宽度为$d=\frac{1}{B}\sqrt{\frac{2mE{y}_{0}}{q}}$;
答:(1)粒子第一次进入磁场时速度的大小为$\sqrt{\frac{2qE{y}_{0}}{m}+{{v}_{0}}^{2}}$;
(2)若要使从y轴上(0,y0)位置以大小不同的初速度沿x轴正方向射入电场的粒子都能经磁场返回电场,则磁场的最小宽度为$\frac{1}{B}\sqrt{\frac{2mE{y}_{0}}{q}}$.
点评 求解带电粒子在磁场中的运动问题时,应用几何关系之前要根据左手定则判断偏转方向才能得到正确的几何关系.


科目:高中物理 来源: 题型:多选题
 如图,质量为M=72kg的重物放置在水平地面上,柔软不可伸长的轻绳跨过光滑轻质滑轮,绳一端连接重物,另一端被质量为m=60kg的人抓住,起初绳子恰好处于竖直绷紧状态,人通过抓绳以a=4m/s2的加速度竖直攀升2m,g取10m/s2,则此过程( )
如图,质量为M=72kg的重物放置在水平地面上,柔软不可伸长的轻绳跨过光滑轻质滑轮,绳一端连接重物,另一端被质量为m=60kg的人抓住,起初绳子恰好处于竖直绷紧状态,人通过抓绳以a=4m/s2的加速度竖直攀升2m,g取10m/s2,则此过程( )| A. | 重物的加速度为2m/s2 | B. | 绳子的拉力为840N | ||
| C. | 人的拉力所做功为2380J | D. | 拉力对重物做功的平均功率为700W |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 位移可能在减小 | B. | 速度与位移方向一定相反 | ||
| C. | 回复力一定在增大 | D. | 加速度与速度方向可能相同 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | N点一定经过平衡位置向下运动,与波的传播方向无关 | |
| B. | 若波由M向N传播,N点处于平衡位置上方位移最大处 | |
| C. | 若波由M向N传播,N点经过平衡位置向上运动 | |
| D. | 若波由N向M传播,N点处于平衡位置下方位移最大处 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
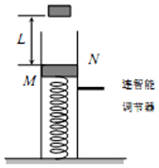 如图所示,质量为m=1kg的长方体金属滑块夹在竖直挡板M、N之间,M、N与金属滑块间动摩擦因数均为μ=0.2,金属滑块与一劲度系数为k=200N/m的轻弹簧相连接,轻弹簧下端固定,挡板M固定不动,挡板N与一智能调节装置相连接(调整挡板与滑块间的压力).起初,滑块静止,挡板与滑块间的压力为0,现有一质量也为m的物体从距滑块L=20cm处自由落下,与滑块瞬间完成碰撞后粘在一起向下运动.为保证滑块下滑过程中做匀减速运动,且下移距离为l=10cm时速度减为0,挡板对滑块的压力须随滑块下移而变化.不计空气阻力,弹簧始终在弹性限度内,g取10m/s2.求:
如图所示,质量为m=1kg的长方体金属滑块夹在竖直挡板M、N之间,M、N与金属滑块间动摩擦因数均为μ=0.2,金属滑块与一劲度系数为k=200N/m的轻弹簧相连接,轻弹簧下端固定,挡板M固定不动,挡板N与一智能调节装置相连接(调整挡板与滑块间的压力).起初,滑块静止,挡板与滑块间的压力为0,现有一质量也为m的物体从距滑块L=20cm处自由落下,与滑块瞬间完成碰撞后粘在一起向下运动.为保证滑块下滑过程中做匀减速运动,且下移距离为l=10cm时速度减为0,挡板对滑块的压力须随滑块下移而变化.不计空气阻力,弹簧始终在弹性限度内,g取10m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
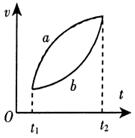 如图,a、b两条对称圆弧曲线分别是汽车甲、乙在同一条平直公路上行驶时的v-t图象,已知在t1时刻两车相遇,a曲线在t1和t2时刻的切线斜率均大于零,则( )
如图,a、b两条对称圆弧曲线分别是汽车甲、乙在同一条平直公路上行驶时的v-t图象,已知在t1时刻两车相遇,a曲线在t1和t2时刻的切线斜率均大于零,则( )| A. | t2时刻两车再次相遇 | |
| B. | 在t1~t2时间内两车平均速度相等 | |
| C. | 甲车速度一直增大,加速度先减小后增大 | |
| D. | 在t1~t2时间内某时刻两车加速度可能相等 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
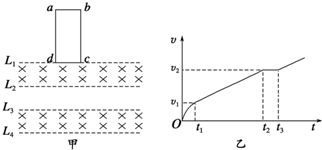
 如图甲所示,在t=0时刻,质量为m,边长为L,电阻为R的正方向金属线框以速度v0进入宽度为L,磁感应强度为B的有界匀强磁场区域,在t=t0时刻,线框恰好全部进入磁场且速度减小为v1;此时刻对线框施加一沿运动方向的力F,使线框在t=2t0时刻恰好完全离开磁场,该过程中线圈的v-t图象如图乙所示,图象关于t=t0对称,下列说法正确的是( )
如图甲所示,在t=0时刻,质量为m,边长为L,电阻为R的正方向金属线框以速度v0进入宽度为L,磁感应强度为B的有界匀强磁场区域,在t=t0时刻,线框恰好全部进入磁场且速度减小为v1;此时刻对线框施加一沿运动方向的力F,使线框在t=2t0时刻恰好完全离开磁场,该过程中线圈的v-t图象如图乙所示,图象关于t=t0对称,下列说法正确的是( )| A. | 线框进入磁场和穿出磁场过程,感应电流方向相同 | |
| B. | 线框进入磁场和穿出磁场的过程,受到安培力方向相同 | |
| C. | 线框进入磁场的过程中,通过导体横截面的电荷量为$\frac{{B{L^2}}}{2R}$ | |
| D. | 线框穿出磁场的过程中,外力F所做的功为m(v02-v12) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com