
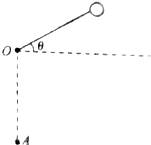
 如图所示,摆球的质量为m,从偏离水平方向θ=30°的位置由静止释放,求:
如图所示,摆球的质量为m,从偏离水平方向θ=30°的位置由静止释放,求:分析 小球开始做自由落体运动,当下落一定高度时绳子绷紧,径向速度由于绳子的作用而消失;绳子沿切向速度前进,此后机械能守恒;结合牛顿第二定律可求得最低点时绳子的拉力.由功能关系可求得总热量.
解答 解:(1)设悬线长为l,下球被释放后,先做自由落体运动,直到下落高度为h=2lsin30°=l,处于松驰状态的细绳被拉直为止.
由机械能守恒定律可知;mgl=$\frac{1}{2}$mv2;
解得:小球的速度竖直向下,大小为$\sqrt{2gl}$.
当绳被拉直时,在绳的冲力作用下,速度v的法向分量减为零(由于绳为理想绳子,能在瞬间产生的极大拉力使球的法向速度减小为零,相应的动能转化为绳的内能);
小球以切向分量开始作变速圆周运动到最低点,v1=vcos30°=$\frac{\sqrt{6gl}}{2}$;
在绳子拉直后的过程中机械能守恒,有mgl(1-sinθ)=$\frac{1}{2}$mv22-$\frac{1}{2}$mv12
在最低点A,根据牛顿第二定律,有
F-mg=m$\frac{{v}_{2}^{2}}{l}$
所以,绳的拉力F=mg+m$\frac{{v}_{2}^{2}}{l}$=3.5mg;
(2)在B点绷紧绳的过程中,由功能关系可知:
Q=$\frac{1}{2}$mv2-$\frac{1}{2}$mv12
解得:Q=$\frac{1}{4}$mgL;
因此小球的机械能不守恒,
答:小球运动到最低点A时绳子受到的拉力是3.5mg;
(2)整个过程中小球的机械能不守恒.
点评 绳子拉直瞬间,物体将损失机械能转化为绳的内能(类似碰撞),本题中很多同学会想当然地认为球初态机械能等于末态机械能,原因是没有分析绳拉直的短暂过程及发生的物理现象.力学问题中的“过程“、“状态“分析是非常重要的,不可粗心忽略.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中物理 来源: 题型:解答题
 如图所示,一小车由半径为R的四分之一光滑圆弧AB和粗糙的足够长的水平部分BC组成,两部分相切于B点,小车质量为M,静止在光滑的水平地面上,一物块质量为m=$\frac{1}{2}$M,从小车上A点处由静止释放,与BC部分动摩擦因数为μ,重力加速度为g,求:
如图所示,一小车由半径为R的四分之一光滑圆弧AB和粗糙的足够长的水平部分BC组成,两部分相切于B点,小车质量为M,静止在光滑的水平地面上,一物块质量为m=$\frac{1}{2}$M,从小车上A点处由静止释放,与BC部分动摩擦因数为μ,重力加速度为g,求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | a粒子受金属核的吸引力在增大 | B. | a粒子加速度在减小 | ||
| C. | a粒子电势能在增加 | D. | a粒子的动能在增大 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
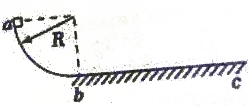 如图所示,质量为m的物块在光滑的$\frac{1}{4}$圆弧轨道的顶端a点由静止开始下滑,圆弧轨道半径为R,最低点b与粗糙水平轨道想接,物块最终滑至c点停止,bc间距为S,求:
如图所示,质量为m的物块在光滑的$\frac{1}{4}$圆弧轨道的顶端a点由静止开始下滑,圆弧轨道半径为R,最低点b与粗糙水平轨道想接,物块最终滑至c点停止,bc间距为S,求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
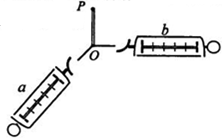 在《互成角度的两个力的合成》这一实验中,如图所示,使b弹簧由图示位置开始缓慢顺时针转动直到接近竖直,在这过程中,保持O点的位置和a弹簧秤的拉伸方向不变,则在整个过程中,关于a、b两弹簧秤示数的变化情况是( )
在《互成角度的两个力的合成》这一实验中,如图所示,使b弹簧由图示位置开始缓慢顺时针转动直到接近竖直,在这过程中,保持O点的位置和a弹簧秤的拉伸方向不变,则在整个过程中,关于a、b两弹簧秤示数的变化情况是( )| A. | a示数增大,b示数增大 | B. | a示数减小,b示数先增大后减小 | ||
| C. | a示数减小,b示数减小 | D. | 示数减小,b示数先减小后增大 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
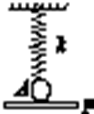 如图所示,劲度系数为k的轻弹簧下端系一个质量为m的小球A,小球被水平挡板P托住使弹簧长度恰为自然长度(小球与挡板不粘连),然后使挡板P以恒定的加速度a(a<g)开始竖直向下做匀加速直线运动,则( )
如图所示,劲度系数为k的轻弹簧下端系一个质量为m的小球A,小球被水平挡板P托住使弹簧长度恰为自然长度(小球与挡板不粘连),然后使挡板P以恒定的加速度a(a<g)开始竖直向下做匀加速直线运动,则( )| A. | 小球与与挡板分离的时间为t=$\sqrt{\frac{ka}{2m(g-a)}}$ | |
| B. | 小球与与挡板分离的时间为t=$\sqrt{\frac{2m(g-a)}{ka}}$ | |
| C. | 小球从开始运动直到最低点的过程中,小球速度最大时弹簧的伸长量x=$\frac{mg}{k}$ | |
| D. | 小球从开始运动直到最低点的过程中,小球速度最大时弹簧的伸长量x=$\frac{m(g-a)}{k}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com