
 如图所示,在xoy平面内以O为圆心、R0为半径的圆形区域I内有垂直纸面向外的匀强磁场.一质量为m、电荷量为+q的粒子以速度v0从A(R0,0)点沿x轴负方向射入区域I,经过P(0,R0)点,沿y轴正方向进入同心环形区域Ⅱ,为使粒子经过区域Ⅱ后能从Q点回到区域I,需在区域Ⅱ内加一垂直于纸面向里的匀强磁场.已知OQ与x轴负方向成30°角,不计粒子重力.求:
如图所示,在xoy平面内以O为圆心、R0为半径的圆形区域I内有垂直纸面向外的匀强磁场.一质量为m、电荷量为+q的粒子以速度v0从A(R0,0)点沿x轴负方向射入区域I,经过P(0,R0)点,沿y轴正方向进入同心环形区域Ⅱ,为使粒子经过区域Ⅱ后能从Q点回到区域I,需在区域Ⅱ内加一垂直于纸面向里的匀强磁场.已知OQ与x轴负方向成30°角,不计粒子重力.求:分析 (1)粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律可以求出粒子的轨道半径,应用牛顿第二定律可以求出磁感应强度.
(2)粒子在磁场中做匀速圆周运动,由几何知识求出边界半径.
(3)求出粒子在磁场中的转过的圆心角,根据粒子做圆周运动的周期公式求出粒子的时间.
解答 解:(1)设在区域Ⅰ内轨迹圆半径为r1,由图中几何关系可得:r1=R0
由牛顿第二定律可得:r1=$\frac{m{v}_{0}}{q{B}_{1}}$
解得:B0=$\frac{m{v}_{0}}{q{R}_{0}}$
(2)设粒子在区域Ⅱ中的轨迹圆半径为r2,部分轨迹如图所示,有几何关系知: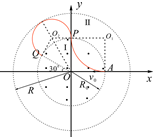 r2=$\frac{\sqrt{3}}{3}{r}_{1}$=$\frac{\sqrt{3}}{3}{R}_{0}$ (1,
r2=$\frac{\sqrt{3}}{3}{r}_{1}$=$\frac{\sqrt{3}}{3}{R}_{0}$ (1,
由几何关系得R=2r2+r2=3r2
即R=$\sqrt{3}{R}_{0}$
(3)当粒子由内侧劣弧经过A点时,应满足
150°n+90°=360°m
当m=4时,n=9时间最短
t1=10($\frac{1}{4}•\frac{2π{R}_{0}}{{v}_{0}})$
t2=9$(\frac{2}{3}•\frac{2π\frac{\sqrt{3}}{3}{R}_{0}}{{v}_{0}})$
最小时间t=t1+t2=$\frac{5π{R}_{0}}{{v}_{0}}$$+\frac{4\sqrt{3}π{R}_{0}}{{v}_{0}}$
答:
(1)区域I中磁感应强度B0的大小为$\frac{m{v}_{0}}{q{R}_{0}}$;
(2)环形区域Ⅱ的外圆半径R至少为$\sqrt{3}{R}_{0}$;
(3)粒子从A点出发到再次经过A点所用的最短时间为$\frac{5π{R}_{0}}{{v}_{0}}$$+\frac{4\sqrt{3}π{R}_{0}}{{v}_{0}}$.
点评 本题考查了粒子在磁场中的运动,分析清楚粒子运动过程,应用牛顿第二定律与周期公式分析答题,作出粒子运动轨迹有助于解题.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中物理 来源: 题型:选择题
| A. | 万有引力定律是卡文迪许发现的 | |
| B. | 万有引力定律公式F=G$\frac{Mm}{{r}^{2}}$中的G是一个比例常数,是没有单位的 | |
| C. | 万有引力定律适用于自然界中的任何两个物体之间 | |
| D. | 万有引力定律公式F=G$\frac{Mm}{{r}^{2}}$表明当r等于零时,万有引力为无穷大 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | α粒子散射实验表明了原子核具有复杂结构 | |
| B. | 石墨在反应堆起到降低核反应速度的作用 | |
| C. | 燃料铀在反应堆中发生裂变反应 | |
| D. | 将镉棒插入得更深些,反应堆的核反应速度将降低 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图,在一二象限内-R≤x≤R范围内有竖直向下的运强电场E,电场的下边界方程为y=$\frac{1}{2R}$x2.在三四象限内存在垂直于纸面向外、边界方程为x2+y2=R2的匀强磁场.匀强磁场的磁感应强度可控制可调节,在第二象限中电场的下边界有许多质量为m,电量为q的正离子,在y=$\frac{1}{2}$R处有一荧光屏,当正离子达到荧光屏时会发光,不计重力和离子间相互作用力.
如图,在一二象限内-R≤x≤R范围内有竖直向下的运强电场E,电场的下边界方程为y=$\frac{1}{2R}$x2.在三四象限内存在垂直于纸面向外、边界方程为x2+y2=R2的匀强磁场.匀强磁场的磁感应强度可控制可调节,在第二象限中电场的下边界有许多质量为m,电量为q的正离子,在y=$\frac{1}{2}$R处有一荧光屏,当正离子达到荧光屏时会发光,不计重力和离子间相互作用力.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 我国的“嫦娥工程”取得了初步的成功.如图所示,假设月球半径为R,飞船在距月球表面高度为3R的圆形轨道Ⅰ上运动,到达轨道的A点点火变轨进入椭圆轨道Ⅱ,到达轨道的近地点B再次点火变轨进入月球近月轨道Ⅲ绕月球做圆周运动,则下列说法正确的是( )
我国的“嫦娥工程”取得了初步的成功.如图所示,假设月球半径为R,飞船在距月球表面高度为3R的圆形轨道Ⅰ上运动,到达轨道的A点点火变轨进入椭圆轨道Ⅱ,到达轨道的近地点B再次点火变轨进入月球近月轨道Ⅲ绕月球做圆周运动,则下列说法正确的是( )| A. | 飞船在轨道Ⅰ的运动速率大于飞船在轨道Ⅲ的运动速率 | |
| B. | 在A处,飞船变轨后瞬间的动能大于变轨前瞬间的动能 | |
| C. | 在B处,飞船变轨后瞬间的动能小于变轨前瞬间的动能 | |
| D. | 飞船在轨道Ⅲ绕月球运行一周所需时间大于在轨道Ⅱ绕月运行一周所需时间 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,在区域Ⅰ和区域Ⅱ内分别存在与纸面垂直的匀强磁场,一带电粒子沿着弧线apb由区域I运动到区域Ⅱ.已知圆弧ap与圆弧pb的弧长之比为2:1,下列说法正确的是( )
如图所示,在区域Ⅰ和区域Ⅱ内分别存在与纸面垂直的匀强磁场,一带电粒子沿着弧线apb由区域I运动到区域Ⅱ.已知圆弧ap与圆弧pb的弧长之比为2:1,下列说法正确的是( )| A. | 粒子在区域I和区域II中的速率之比为2:1 | |
| B. | 粒子通过圆弧ap、pb的时间之比为2:1 | |
| C. | 圆弧ap与圆弧pb对应的圆心角之比为2:1 | |
| D. | 区域I和区域II的磁感应强度方向相反 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com