
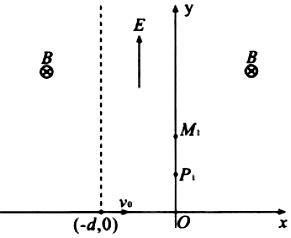
���� ��1������ƽ���˶��õ������ڵ糡�е��˶����ɣ��õ��糡��ǿ�ı���ʽ�����������ڴų��е��˶����ڱ߽紦�öԳ��Եõ��Ÿ�Ӧǿ�ȵı���ʽ��
��2���������ӵ��˶�����������ӵ��˶��ֽ⣬��������ڵ����ν����Ҳ�ų�ʱ���ٶȴ�С�������ݴ��������ڴų��е��˶����ɼ����ӵ�y����Զ����ʱ���˶�λ�ý��������룮
��� �⣺��1�������ڵ糡���ܵ���ֱ���ϵĵ糡��F=qE�����ٶ�$a=\frac{F}{m}=\frac{qE}{m}$��
���Ӵ�y���ϵ�${P}_{1}��0��\frac{d}{2}��$���һ���뿪�糡�����У�$\frac{d}{2}=\frac{1}{2}��\frac{qE}{m}����\frac{d}{{v}_{0}}��^{2}$�����ԣ�$E=\frac{m{{v}_{0}}^{2}}{qd}$��
�����ӵ�һ�ν���ų�ʱ���ٶ�Ϊv����v��ˮƽ����vx=v0����ֱ����${v}_{y}=at=\frac{qEd}{m{v}_{0}}$=v0������$v=\sqrt{2}{v}_{0}$��
�����ڴų����˶�������������Ϊ��������$Bvq=\frac{m{v}^{2}}{R}$����$B=\frac{mv}{qR}$��
���ٶ�v�ķ����֪����M1P1Q=45�㣬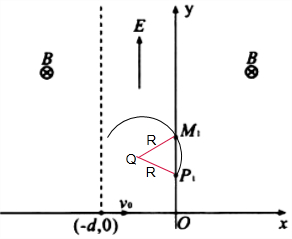 ��
��
����Բ������������ĶԳ��Կ�֪��$R=\frac{\frac{1}{2}{M}_{1}{P}_{1}}{cos��{M}_{1}{P}_{1}Q}=\frac{\frac{1}{2}��\frac{1}{2}d}{\frac{\sqrt{2}}{2}}=\frac{\sqrt{2}}{4}d$��
���ԣ�$B=\frac{mv}{qR}=\frac{\sqrt{2}m{v}_{0}}{\frac{\sqrt{2}}{4}qd}=\frac{4m{v}_{0}}{qd}$��
���ԣ�$\frac{E}{B}=\frac{\frac{m{{v}_{0}}^{2}}{qd}}{\frac{4m{v}_{0}}{qd}}=\frac{{v}_{0}}{4}$��
��2����������Բ���˶��ĶԳ��Կ�֪�������ӽ���ų�ʱ��ֱ�߽���ٶȷ���Ϊv1��ƽ�б߽���ٶȷ���Ϊv2���������뿪�ų�ʱ��v1����v2���䣻
�����ڵ糡��ֻ�ܵ糡��������������ƽ���˶���
���ԣ����ӵ�3�ν����Ҳ�ų���x��0��ʱ���ٶȵ�ˮƽ����v3x=v0��
��ֱ������ٶȾ����ų�û�иı䣬�ڵ糡�м��ٶȲ��䣬���Ӿ���5�ε糡�ŵ�3�ν����Ҳ�ų���x��0����ÿ�ξ����糡��ʱ�䶼��ͬ��
���ԣ�${v}_{3y}=5at=5��\frac{qE}{m}��\frac{d}{{v}_{0}}=\frac{5qEd}{m{v}_{0}}=5{v}_{0}$��
���ԣ�${v}_{3}=\sqrt{{{v}_{3x}}^{2}+{{v}_{3y}}^{2}}=\sqrt{26}{v}_{0}$��$r=\frac{m{v}_{3}}{Bq}=\frac{\sqrt{26}}{4}d$��
��v3�ķ���ɵ������ڴų�����ͼ��ʾ�˶���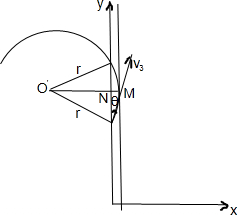 ��
��
������M����ƽ����y���ֱ�����У����ԣ�M��Ϊ���ӵ�3�����Ҳ�ų���x��0���˶��Ĺ����У���y�����Զ����NM��
����$tan��=\frac{{v}_{3x}}{{v}_{3y}}=\frac{1}{5}$�����ԣ�$cos��=\frac{5\sqrt{26}}{26}$��NM=O��M-O��N=r-rcos��=r��1-cos�ȣ�=$\frac{\sqrt{26}}{4}d����1-\frac{5\sqrt{26}}{26}��=\frac{\sqrt{26}-5}{4}d$��
�𣺣�1���糡ǿ��E�ʹŸ�Ӧǿ��B�ı�ֵΪ$\frac{{v}_{0}}{4}$��
��2�����ӵ�3�����Ҳ�ų���x��0���˶��Ĺ����У���y�����Զ����Ϊ$\frac{\sqrt{26}-5}{4}d$��
���� �ڴ������ӽ����ų��������ϣ����Գ�����öԳ�����⣬�����ӽ���ų�ʱ��ֱ�߽���ٶȷ���Ϊv1��ƽ�б߽���ٶȷ���Ϊv2���������뿪�ų�ʱ��v1����v2���䣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
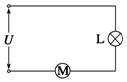 ����ͼ��ʾ�ĵ�·�У������ѹU��Ϊ8V������L���С�3V��6W���������綯����Ȧ�ĵ���RM=1����������ǡ���������⣬����˵����ȷ���ǣ�������
����ͼ��ʾ�ĵ�·�У������ѹU��Ϊ8V������L���С�3V��6W���������綯����Ȧ�ĵ���RM=1����������ǡ���������⣬����˵����ȷ���ǣ�������| A�� | �綯���������ѹ��5 V | B�� | �綯����Ч����80% | ||
| C�� | ͨ���綯���ĵ�����2 A | D�� | ������·���ĵĵ繦����16 W |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ͼ��a����ʾ�������պ�Բ����ȦA��B��Բ���غϣ�����ͬһˮƽ���ڣ���ȦA��ͨ����ͼ��b����ʾ�Ľ��������t=0ʱ��������Ϊ˳ʱ�루��ͼ��ͷ��ʾ����t1-t2ʱ����ڣ�������ȦB������˵���д�����ǣ�������
��ͼ��a����ʾ�������պ�Բ����ȦA��B��Բ���غϣ�����ͬһˮƽ���ڣ���ȦA��ͨ����ͼ��b����ʾ�Ľ��������t=0ʱ��������Ϊ˳ʱ�루��ͼ��ͷ��ʾ����t1-t2ʱ����ڣ�������ȦB������˵���д�����ǣ�������| A�� | ��ȦB����˳ʱ�뷽��ĵ�������Ȧ�����ŵ����� | |
| B�� | ��ȦB����˳ʱ�뷽��ĵ�������Ȧ������������ | |
| C�� | ��ȦB������ʱ�뷽��ĵ�������Ȧ�����ŵ����� | |
| D�� | ��ȦB������ʱ�뷽��ĵ�������Ȧ������������ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ͼ�������ƽ�еij�ֱ���߷ֱ�ͨ�з����෴�ĵ���I1��I2��A��B��C��DΪ����ijһ��������ڵ�ƽ���ڵ��ĵ㣬��A��B��C�������߹��棬B����������֮�䣬B��D�������뵼������ƽ�洹ֱ���Ÿ�Ӧǿ�ȿ���Ϊ��ĵ��ǣ�������
��ͼ�������ƽ�еij�ֱ���߷ֱ�ͨ�з����෴�ĵ���I1��I2��A��B��C��DΪ����ijһ��������ڵ�ƽ���ڵ��ĵ㣬��A��B��C�������߹��棬B����������֮�䣬B��D�������뵼������ƽ�洹ֱ���Ÿ�Ӧǿ�ȿ���Ϊ��ĵ��ǣ�������| A�� | A�� | B�� | B�� | C�� | C�� | D�� | D�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ����xOyƽ������һ�뾶Ϊr��Բ�δų��������ڷֲ��ŴŸ�Ӧǿ��ΪB����ֱֽ���������ǿ�ų���Բ������߽��Ϸ���Բ�εĸй⽺Ƭ�����Ӵ������ϻ�й⣮�ڴų��߽���x�ύ��A����һ����ԴA����������Ϊm������Ϊq�������ش�ֱ�ų��������ų����䷽��ֲ�����AB��AC���нǶ��ڣ�B��CΪ�����߽���y����������㣮�����㹻����ʱ�䣬������ȫ�����ڵڢ����ĸй⽺Ƭ�ϣ�����Щ�������ٶ������ǣ�������
��ͼ��ʾ����xOyƽ������һ�뾶Ϊr��Բ�δų��������ڷֲ��ŴŸ�Ӧǿ��ΪB����ֱֽ���������ǿ�ų���Բ������߽��Ϸ���Բ�εĸй⽺Ƭ�����Ӵ������ϻ�й⣮�ڴų��߽���x�ύ��A����һ����ԴA����������Ϊm������Ϊq�������ش�ֱ�ų��������ų����䷽��ֲ�����AB��AC���нǶ��ڣ�B��CΪ�����߽���y����������㣮�����㹻����ʱ�䣬������ȫ�����ڵڢ����ĸй⽺Ƭ�ϣ�����Щ�������ٶ������ǣ�������| A�� | v=$\frac{\sqrt{2}Bqr}{2m}$ | B�� | v=$\frac{Bqr}{m}$ | C�� | v=$\frac{\sqrt{2}Bqr}{m}$ | D�� | v=$\frac{��2+\sqrt{2}��Bqr}{m}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ��·�У���Դ��ѹu=311sin ��100��t�� V��A��B����С�220V440W���ĵ�ů������220V 220W���ij����̻���������ѹ��������˿������˵����ȷ���ǣ�������
��ͼ��ʾ��·�У���Դ��ѹu=311sin ��100��t�� V��A��B����С�220V440W���ĵ�ů������220V 220W���ij����̻���������ѹ��������˿������˵����ȷ���ǣ�������| A�� | ��·Ҫ��������������˿�Ķ��������С��3 A | |
| B�� | ������ѹ����ʾ��Ϊ311 V | |
| C�� | ��ů�����ȹ����dz����̻����ȹ��ʵ�2�� | |
| D�� | 1 min�ڳ����̻�����������Ϊ1.32��104 J |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
 ��ͼ��ʾ����L=4m�Ĵֲ�ˮƽֱ���AB��뾶R=0.8m�Ĺ⻬$\frac{1}{4}$Բ�����BC������BΪԲ������͵㣬CΪ$\frac{1}{4}$Բ����������m1=1kg�����徲ֹ��A�㣬m1��ˮƽ����Ķ�Ħ��������=0.2������m2=2kg�����徲ֹ��B�㣬A��B����Ϊ�ʵ㣬������ˮƽ����ɦ�=37��ĺ���F��m1��ʼ�����˶����˶�x1=2.5m��ȥ����F��m1�˶���B����m2��ײ����ײ����ʱ����Բ��ƣ�������m1������������x2=0.25m��ֹ��m2��C��ʱ��Բ����������ǡ�õ����㣬g=10m/s2����
��ͼ��ʾ����L=4m�Ĵֲ�ˮƽֱ���AB��뾶R=0.8m�Ĺ⻬$\frac{1}{4}$Բ�����BC������BΪԲ������͵㣬CΪ$\frac{1}{4}$Բ����������m1=1kg�����徲ֹ��A�㣬m1��ˮƽ����Ķ�Ħ��������=0.2������m2=2kg�����徲ֹ��B�㣬A��B����Ϊ�ʵ㣬������ˮƽ����ɦ�=37��ĺ���F��m1��ʼ�����˶����˶�x1=2.5m��ȥ����F��m1�˶���B����m2��ײ����ײ����ʱ����Բ��ƣ�������m1������������x2=0.25m��ֹ��m2��C��ʱ��Բ����������ǡ�õ����㣬g=10m/s2�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
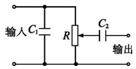 ��ͼ��ʾΪij�����е�·��һ���֣���������ֱ���ɷ֡�������Ƶ�ɷֺͽ�����Ƶ�ɷֵĵ�������������˵õ��ɵ���С�Ľ�����Ƶ�ɷ֣���ô�����йظ�Ԫ���������õ�˵���У�������ǣ�������
��ͼ��ʾΪij�����е�·��һ���֣���������ֱ���ɷ֡�������Ƶ�ɷֺͽ�����Ƶ�ɷֵĵ�������������˵õ��ɵ���С�Ľ�����Ƶ�ɷ֣���ô�����йظ�Ԫ���������õ�˵���У�������ǣ�������| A�� | C1Ϊ��Ƶ��·��������������Ƶ�ɷֱ��õ�������· | |
| B�� | RΪ���������������Ļ�Ƭ�����ƶ����Ըı�����˵�ѹ�Ĵ�С | |
| C�� | C2Ϊ��ֱ��������������Ƶ�ɷ�ͨ���õ�������� | |
| D�� | C1�ĵ��ݽϴ�C2�ĵ��ݽ�С |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼʾ��·�У������ĵ�����G1 ��G2����㶼�ڿ̶������룬�������ӡ�+������������ʱ��ָ�����Ұڣ������ӡ�-������������ʱ��ָ������ڣ��ڵ�·��ͨ�ȶ�������������ʾ����ΪI���ֿ���S��ԭ���պ�״̬ͻȻ�Ͽ�����S�Ͽ���˲�䣬G1����ָ������ƫ��G2����ָ������ƫ��������ҡ�����ͨ��G2���ĵ�����СΪI��
��ͼʾ��·�У������ĵ�����G1 ��G2����㶼�ڿ̶������룬�������ӡ�+������������ʱ��ָ�����Ұڣ������ӡ�-������������ʱ��ָ������ڣ��ڵ�·��ͨ�ȶ�������������ʾ����ΪI���ֿ���S��ԭ���պ�״̬ͻȻ�Ͽ�����S�Ͽ���˲�䣬G1����ָ������ƫ��G2����ָ������ƫ��������ҡ�����ͨ��G2���ĵ�����СΪI���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com