

| y |
| x |
| 1 |
| 2 |
| 2gh |
| y |
| x |
| ||
| v0t |
| gt |
| 2v0 |
| 1 |
| 2 |
| x2+y2 |
| y |
| x |
| ||
| v0t |
| gt |
| 2v0 |
| 1 |
| 2 |
| 1 |
| 2 |
| v02+vy2 |



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中物理 来源: 题型:

查看答案和解析>>
科目:高中物理 来源: 题型:
查看答案和解析>>
科目:高中物理 来源: 题型:
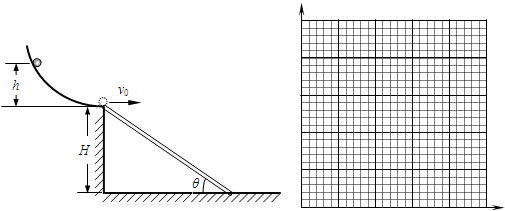
 光滑曲面轨道末端切线水平,一长度合适的木板两端分别搁在轨道末端点和水平地面间,构成倾角为
光滑曲面轨道末端切线水平,一长度合适的木板两端分别搁在轨道末端点和水平地面间,构成倾角为![]() 的斜面,如图所示。一可视作质点的质量为m=1kg的小球,从距离轨道末端点竖直高度为h=0.2m处由静止开始滑下。(不计空气阻力,g取10m/s2,
的斜面,如图所示。一可视作质点的质量为m=1kg的小球,从距离轨道末端点竖直高度为h=0.2m处由静止开始滑下。(不计空气阻力,g取10m/s2,![]() ,
,![]() )
)
(1)求小球从轨道末端点冲出瞬间的速度v0的大小;
 (2)若改变木板长度,并使木板两端始终与平台和水平面相接,试通过计算推导小球第一次撞击木板时的动能随木板倾角
(2)若改变木板长度,并使木板两端始终与平台和水平面相接,试通过计算推导小球第一次撞击木板时的动能随木板倾角![]() 变化的关系式,并在图中作出
变化的关系式,并在图中作出![]() 图象。
图象。
查看答案和解析>>
科目:高中物理 来源:2011年江苏省普通高中学业水平考试物理模拟试卷(二)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com