
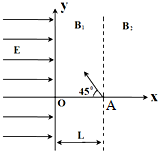
 在直角坐标系的二、三象限内有沿x轴正向的匀强电场,场强大小为E,在一、四象限内以x=L的直线为理想边界的左右两侧存在垂直于纸面向里的匀强磁场B1和B2,y轴为电场与磁场的理想边界.在x轴上x=L的A点有一个质量为m、带电荷量为+q的粒子以速度v沿与x轴负方向成45°的夹角垂直于磁场射出.粒子到达y轴时速度方向与y轴刚好垂直.若带电粒子经历在电场和磁场中的一系列运动后刚好能够返回A点.不计粒子的重力
在直角坐标系的二、三象限内有沿x轴正向的匀强电场,场强大小为E,在一、四象限内以x=L的直线为理想边界的左右两侧存在垂直于纸面向里的匀强磁场B1和B2,y轴为电场与磁场的理想边界.在x轴上x=L的A点有一个质量为m、带电荷量为+q的粒子以速度v沿与x轴负方向成45°的夹角垂直于磁场射出.粒子到达y轴时速度方向与y轴刚好垂直.若带电粒子经历在电场和磁场中的一系列运动后刚好能够返回A点.不计粒子的重力分析 (1)根据题设条件粒子带正电从A点射入磁场,能垂直打在y轴上,粒子做匀速圆周运动,洛伦兹力提供向心力,根据几何关系求出半径,即可求出${B}_{1}^{\;}$
(2)作出粒子运动轨迹,在电场中做匀变速直线运动,在磁场中做匀速圆周运动,分别求出在电场中运动的时间和在磁场${B}_{1}^{\;}$中运动的时间,即可求解;
(3)考虑到带电粒子经历在电场和磁场中的一系列运动后刚好能够返回A点,在磁场${B}_{2}^{\;}$中,只要满足n△y=2OP带电粒子就能够返回A点,再结合向心力方程联立即可求解.
解答 解:(1)设带电粒子在磁场B1中的运动半径为R1,根据题意有:${R}_{1}^{\;}sin45°=L$
洛伦兹力提供向心力,有:${B}_{1}^{\;}qv=m\frac{{v}_{\;}^{2}}{{R}_{1}^{\;}}$
解得:${B}_{1}^{\;}=\frac{\sqrt{2}mv}{2qL}$
(2)粒子在磁场B1中的运动周期为:${T}_{1}^{\;}=\frac{2πm}{q{B}_{1}^{\;}}$
粒子在磁场B1中的运动时间为:${t}_{1}^{\;}=\frac{1}{4}{T}_{1}^{\;}$
粒子在电场中运动的加速度为:$a=\frac{qE}{m}$
粒子在电场中匀减速运动和匀加速运动的时间相等,则时间为:${t}_{2}^{\;}=\frac{2v}{a}$
粒子从A点出发到第一次返回到直线x=L上的时间为:
$t={t}_{1}^{\;}+{t}_{2}^{\;}=\frac{\sqrt{2}πL}{2v}+\frac{2mv}{qE}$
(3)如图所示,设带电粒子在磁场B2中的运动半径为R2,带电粒子第一次出B2磁场的位置和A点的距离为△y,有:
$△y=\sqrt{2}{R}_{2}^{\;}-2OP$
而$OP={R}_{1}^{\;}-L$
只要满足n△y=2OP带电粒子就能够返回A点
即$n[\sqrt{2}{R}_{2}^{\;}-2(\sqrt{2}-1)L]=2(\sqrt{2}-1)L$
解得${R}_{2}^{\;}=(1+\frac{1}{n})(2-\sqrt{2})L$
又由向心力方程${B}_{2}^{\;}qv=m\frac{{v}_{\;}^{2}}{{R}_{2}^{\;}}$
得${B}_{2}^{\;}=\frac{n(2+\sqrt{2})mv}{2(n+1)qL}$ (n=1,2,3,…)
答:(1)B1的大小为$\frac{\sqrt{2}mv}{2qL}$;
(2)粒子从A点出发到第一次返回到直线x=L上的时间$\frac{\sqrt{2}πL}{2v}+\frac{2mv}{qE}$;
(3)B2大小的可能值$\frac{n(2+\sqrt{2})mv}{2(n+1)qL}$(n=1,2,3,…)
点评 本题难点是根据题目给出的物理情境作出粒子运动的轨迹示意图,由图象根据几何关系求出粒子在两个磁场中运动的半径与已知量的关系,多过程中分析,需要细心细致的求解.


 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:高中物理 来源: 题型:多选题
| A. | 物体速度不为零,其加速度也一定不为零 | |
| B. | 物体具有加速度时,它的速度可能不会改变 | |
| C. | 物体的加速度变大时,速度也一定随之变大 | |
| D. | 物体加速度方向改变时,速度方向可以保持不变 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 某同学在科技馆做“水对不同形状运动物体的阻力大小的比较”实验,图甲中两个完全相同的浮块,头尾相反放置在同一起始线上,它们通过细线与终点的电动机连接.两浮块分别在大小为F的二个相同牵引力作用下同时开始向终点作直线运动,运动过程中该同学摄得照片如图乙.已知拍下乙图时,左侧浮块运动的距离恰好为右侧浮块运动距离的2倍,假设从浮块开始运动到拍下照片的过程中,浮块受到的阻力不变,试求该过程中:
某同学在科技馆做“水对不同形状运动物体的阻力大小的比较”实验,图甲中两个完全相同的浮块,头尾相反放置在同一起始线上,它们通过细线与终点的电动机连接.两浮块分别在大小为F的二个相同牵引力作用下同时开始向终点作直线运动,运动过程中该同学摄得照片如图乙.已知拍下乙图时,左侧浮块运动的距离恰好为右侧浮块运动距离的2倍,假设从浮块开始运动到拍下照片的过程中,浮块受到的阻力不变,试求该过程中:查看答案和解析>>
科目:高中物理 来源: 题型:计算题

查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图,两个初速度大小相同的不同粒子a和b,从O点沿垂直磁场方向进入匀强磁场,最后都打到屏上P点.不计重力.下列说法正确的有( )
如图,两个初速度大小相同的不同粒子a和b,从O点沿垂直磁场方向进入匀强磁场,最后都打到屏上P点.不计重力.下列说法正确的有( )| A. | a、b均带负电 | |
| B. | a在磁场中飞行的时间比b的短 | |
| C. | a在磁场做匀速圆周运支的角速度比b的大 | |
| D. | a的比荷($\frac{q}{m}$)比b小 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
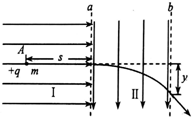 如图所示,虚线a左侧有水平向右的匀强电场Ⅰ,距离为L的虚线a、b之间有竖直向下的匀强电场Ⅱ,电场Ⅰ、Ⅱ的场强分别为2E、E.将一个质量为m、电荷量为+q的带电粒子从图中A点由静止释放,已知A点到虚线a的距离为s,忽略粒子所受重力,求:
如图所示,虚线a左侧有水平向右的匀强电场Ⅰ,距离为L的虚线a、b之间有竖直向下的匀强电场Ⅱ,电场Ⅰ、Ⅱ的场强分别为2E、E.将一个质量为m、电荷量为+q的带电粒子从图中A点由静止释放,已知A点到虚线a的距离为s,忽略粒子所受重力,求:查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图,在匀强磁场中有一倾斜的平行光滑金属导轨,导轨间距为L=30cm,长度为d=l00cm,导轨平面与水平面的夹角为θ=37°匀强磁场的磁感应强度大小为B=2.0T,方向与导轨平面垂直.质量m=60g,电阻r=0.5Ω的导体棒从导轨的顶端由静止释放,在滑到导轨底端之前已经达到最大速度.导体棒始终与导轨垂直,接在两导轨间的电阻为R=1.5Ω,导轨电阻不计,重加速度为g=10m/s2,sin37°=0.6.求:
如图,在匀强磁场中有一倾斜的平行光滑金属导轨,导轨间距为L=30cm,长度为d=l00cm,导轨平面与水平面的夹角为θ=37°匀强磁场的磁感应强度大小为B=2.0T,方向与导轨平面垂直.质量m=60g,电阻r=0.5Ω的导体棒从导轨的顶端由静止释放,在滑到导轨底端之前已经达到最大速度.导体棒始终与导轨垂直,接在两导轨间的电阻为R=1.5Ω,导轨电阻不计,重加速度为g=10m/s2,sin37°=0.6.求:查看答案和解析>>
科目:高中物理 来源: 题型:实验题
 实验室备有以下器材:
实验室备有以下器材:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com