
分析 想要测量木星的质量,需要知道卫星绕木星做圆周运动的轨道半径和周期,结合万有引力提供向心力求出木星的质量.
解答 解:(1)需要测量卫星绕木星做圆周运动的轨道半径r和周期T.
(2)根据$G\frac{Mm}{{r}^{2}}=mr\frac{4{π}^{2}}{{T}^{2}}$得,木星的质量M=$\frac{4{π}^{2}{r}^{3}}{G{T}^{2}}$.
答:(1)需要测量卫星绕木星做圆周运动的轨道半径r和周期T.
(2)木星的质量为$\frac{4{π}^{2}{r}^{3}}{G{T}^{2}}$.
点评 解决本题的关键掌握万有引力提供向心力这一重要理论,知道根据该理论只能求出中心天体质量,不能求解环绕天体的质量.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中物理 来源: 题型:选择题
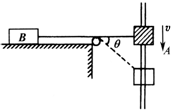 如图所示,开始时A.B间的细绳呈水平状态,现使物体A以速度v沿杆匀速下滑,经细绳通过定滑轮拉物体B,当绳与水平方向的夹角为θ时,物体B的速度为( )
如图所示,开始时A.B间的细绳呈水平状态,现使物体A以速度v沿杆匀速下滑,经细绳通过定滑轮拉物体B,当绳与水平方向的夹角为θ时,物体B的速度为( )| A. | vcosθ | B. | vsinθ | C. | $\frac{v}{cosθ}$ | D. | $\frac{v}{sinθ}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,真空中同一平面内MN直线上固定电荷量分别为-9Q和+Q的两个点电荷,两者相距为L,以+Q点电荷为圆心,半径为 $\frac{L}{2}$ 画圆,a、b、c、d是圆周上四点,其中a、b在MN直线上,c、d两点连线垂直于MN,一电荷量为q的负点电荷在圆周上运动,比较a、b、c、d四点,则下列说法错误的是( )
如图所示,真空中同一平面内MN直线上固定电荷量分别为-9Q和+Q的两个点电荷,两者相距为L,以+Q点电荷为圆心,半径为 $\frac{L}{2}$ 画圆,a、b、c、d是圆周上四点,其中a、b在MN直线上,c、d两点连线垂直于MN,一电荷量为q的负点电荷在圆周上运动,比较a、b、c、d四点,则下列说法错误的是( )| A. | 在a点电场强度最大 | B. | 电荷q在b点的电势能最大 | ||
| C. | 在c、d两点的电势相等 | D. | 电荷q在a点的电势能最大 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
 国际乒联为使乒乓球在比赛中的来回次数增加,提高比赛的观赏性,将比赛用球的直径从原来的38mm增大到40mm,质量由原来的2.5克增加到2.7克.研究人员称,40mm大球比原38mm小球旋转减弱$\frac{1}{5}$,速度减慢$\frac{1}{7}$,弹性也有所下降.小李为了比较新、老标准乒乓球的运动特性,他请另一同学将一只直径40mm的大球和一只直径38mm的小球,从同一高处同时自由落下,在两球下落过程中,他用照相机拍摄到两球下落过程中一段径迹的照片,如图所示,背景中的横虚线是竖直墙面上两块磁砖的接逢处.拍摄时所用快门速度为$\frac{1}{30}$秒,则:
国际乒联为使乒乓球在比赛中的来回次数增加,提高比赛的观赏性,将比赛用球的直径从原来的38mm增大到40mm,质量由原来的2.5克增加到2.7克.研究人员称,40mm大球比原38mm小球旋转减弱$\frac{1}{5}$,速度减慢$\frac{1}{7}$,弹性也有所下降.小李为了比较新、老标准乒乓球的运动特性,他请另一同学将一只直径40mm的大球和一只直径38mm的小球,从同一高处同时自由落下,在两球下落过程中,他用照相机拍摄到两球下落过程中一段径迹的照片,如图所示,背景中的横虚线是竖直墙面上两块磁砖的接逢处.拍摄时所用快门速度为$\frac{1}{30}$秒,则:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | $\frac{{4{π^2}{r^3}}}{{G{T^2}}}$ | B. | $\frac{{3π{R^3}}}{{G{T^2}{r^3}}}$ | C. | $\frac{{3π{r^3}}}{{G{T^2}{R^3}}}$ | D. | $\frac{3π}{{G{T^2}}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
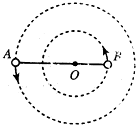 神奇的黑洞是近代引力理论所预言的一种特殊天体,探寻黑洞的方案之一是观测双星系统的运动规律.天文学家观测河外星系大麦哲伦云时,发现了LMCX-3双星系统,它由可见星A和不可见的暗星B构成.两星视为质点,不考虑其他天体的影响,A、B围绕两者连线上的O点做匀速圆周运动,它们之间的距离保持不变,如图所示.引力常量为G,由观测能够得到可见星A的速率v和运行周期T.
神奇的黑洞是近代引力理论所预言的一种特殊天体,探寻黑洞的方案之一是观测双星系统的运动规律.天文学家观测河外星系大麦哲伦云时,发现了LMCX-3双星系统,它由可见星A和不可见的暗星B构成.两星视为质点,不考虑其他天体的影响,A、B围绕两者连线上的O点做匀速圆周运动,它们之间的距离保持不变,如图所示.引力常量为G,由观测能够得到可见星A的速率v和运行周期T.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com