
 一带有乒乓球发射机的乒乓球台如图所示,水平台面的长和宽分别为L1和L2,中间球网高度为h,发射机安装于台面左侧边缘的中点,能以不同速率向右侧不同方向水平发射乒乓球,发射点距台面高度为3h,不计空气的作用,重力加速度大小为g,若乒乓球的发射率v在某范围内,通过选择合适的方向,就能使乒乓球落到球网右侧台面上,到v的最大取值范围是( )
一带有乒乓球发射机的乒乓球台如图所示,水平台面的长和宽分别为L1和L2,中间球网高度为h,发射机安装于台面左侧边缘的中点,能以不同速率向右侧不同方向水平发射乒乓球,发射点距台面高度为3h,不计空气的作用,重力加速度大小为g,若乒乓球的发射率v在某范围内,通过选择合适的方向,就能使乒乓球落到球网右侧台面上,到v的最大取值范围是( )| A. | $\frac{{L}_{1}}{2}$$\sqrt{\frac{g}{6h}}$<v<L1$\sqrt{\frac{g}{6h}}$ | B. | $\frac{{L}_{1}}{4}$$\sqrt{\frac{g}{h}}$<v<$\sqrt{\frac{(4{L}_{1}^{2}+{L}_{2}^{2})g}{6h}}$ | ||
| C. | $\frac{{L}_{1}}{2}$$\sqrt{\frac{g}{6h}}$<v<$\frac{1}{2}$$\sqrt{\frac{(4{L}_{1}^{2}+{L}_{2}^{2})g}{6h}}$ | D. | $\frac{{L}_{1}}{4}$$\sqrt{\frac{g}{h}}$<v<$\frac{1}{2}$$\sqrt{\frac{(4{L}_{1}^{2}+{L}_{2}^{2})g}{6h}}$ |
分析 球要落在网右侧台面上,临界情况是与球网恰好不相撞,还有与球台边缘相碰,根据高度求出平抛运动的时间,根据几何关系求出最小的水平位移和最大的水平位移,从而得出最小速度和最大速度.
解答 解:若球与网恰好不相碰,根据3h-h=$\frac{1}{2}g{{t}_{1}}^{2}$得,${t}_{1}=\sqrt{\frac{4h}{g}}$,
水平位移的最小值${x}_{min}=\frac{{L}_{1}}{2}$,则最小速度${v}_{1}=\frac{\frac{{L}_{1}}{2}}{{t}_{1}}=\frac{{L}_{1}}{4}\sqrt{\frac{g}{h}}$.
若球与球台边缘相碰,根据3h=$\frac{1}{2}g{{t}_{2}}^{2}$得,${t}_{2}=\sqrt{\frac{6h}{g}}$,
水平位移的最大值为xmax=$\sqrt{{{L}_{1}}^{2}+\frac{{{L}_{2}}^{2}}{4}}$,
则最大速度${v}_{2}=\frac{\sqrt{{{L}_{1}}^{2}+\frac{{{L}_{2}}^{2}}{4}}}{{t}_{2}}=\frac{1}{2}\sqrt{\frac{(4{{L}_{1}}^{2}+{{L}_{2}}^{2})g}{6h}}$,故D正确,A、B、C错误.
故选:D.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,抓住临界情况,结合运动学公式灵活求解,难度中等.


科目:高中物理 来源: 题型:选择题
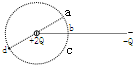 如图所示,真空中同一平面内固定两点电荷+2Q和-Q,以点电荷+2Q为圆心的圆上有a、b、c、d四点,其中b点为两点电荷连线与圆的交点,a、c两点关于连线对称,ad为圆的直径,且d距-Q较远.当电子经过这四点时,下列说法正确的是( )
如图所示,真空中同一平面内固定两点电荷+2Q和-Q,以点电荷+2Q为圆心的圆上有a、b、c、d四点,其中b点为两点电荷连线与圆的交点,a、c两点关于连线对称,ad为圆的直径,且d距-Q较远.当电子经过这四点时,下列说法正确的是( )| A. | 在b处电势能最大 | B. | 在d处电势能最大 | ||
| C. | 在d处所受电场力最大 | D. | 在a、c两处所受电场力相同 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
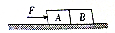 如图所示,质量分别为m1=1kg,m2=2kg的两物块A、B并排放在光滑水平面上,一水平向右的推力F=6N作用在物块A上,在力F的作用下物块A、B由静止开始共同运动了t=2s,求在此过程中物块A对物块B所做的功W.
如图所示,质量分别为m1=1kg,m2=2kg的两物块A、B并排放在光滑水平面上,一水平向右的推力F=6N作用在物块A上,在力F的作用下物块A、B由静止开始共同运动了t=2s,求在此过程中物块A对物块B所做的功W.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
| F(N) | 0 | 0.50 | 1.00 | 1.50 | 2.00 | 2.50 |
| l(cm) | l0 | 10.97 | 12.02 | 13.00 | 13.98 | 15.05 |
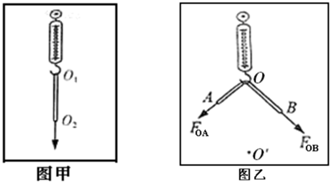
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
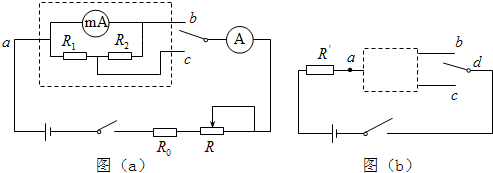
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图,在足够长的光滑水平面上,物体A、B、C位于同一直线上,A点位于B、C之间,A的质量为m,B、C的质量都为M,三者均处于静止状态,现使A以某一速度向右运动,求m和M之间应满足什么条件,才能使A只与B、C各发生一次碰撞.设物体间的碰撞都是弹性的.
如图,在足够长的光滑水平面上,物体A、B、C位于同一直线上,A点位于B、C之间,A的质量为m,B、C的质量都为M,三者均处于静止状态,现使A以某一速度向右运动,求m和M之间应满足什么条件,才能使A只与B、C各发生一次碰撞.设物体间的碰撞都是弹性的.查看答案和解析>>
科目:高中物理 来源: 题型:多选题
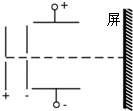 如图所示,氕核、氘核、氚核三种粒子从同一位置无初速地飘入电场线水平向右的加速电场E1,之后进入电场线竖直向下的匀强电场E2发生偏转,最后打在屏上.整个装置处于真空中,不计粒子重力及其相互作用,那么( )
如图所示,氕核、氘核、氚核三种粒子从同一位置无初速地飘入电场线水平向右的加速电场E1,之后进入电场线竖直向下的匀强电场E2发生偏转,最后打在屏上.整个装置处于真空中,不计粒子重力及其相互作用,那么( )| A. | 偏转电场E2对三种粒子做功一样多 | B. | 三种粒子打到屏上时的速度一样大 | ||
| C. | 三种粒子运动到屏上所用时间相同 | D. | 三种粒子一定打到屏上的同一位置 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | $\frac{1}{10}$ | B. | 1 | C. | 5 | D. | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com