
 ͼ��ʾ��һ�������������ʾ��ͼ���߿�abcd������ǿ�ų��У���֪ab=bc=10cm��B=1T����Ȧ����n=100����Ȧ����r=5�������·���ص���R=5������Ȧ��600r/min��ת������ת������
ͼ��ʾ��һ�������������ʾ��ͼ���߿�abcd������ǿ�ų��У���֪ab=bc=10cm��B=1T����Ȧ����n=100����Ȧ����r=5�������·���ص���R=5������Ȧ��600r/min��ת������ת���������� ��1����ѹ����ʾ��Ϊ��Чֵ����������ʽ���������Чֵ��ʽ��ŷķ���ɿ���õ�ѹ����ʾ����
��2�������ֵ�����˲ʱ����ʽ��
��3������$\overline{E}=\frac{n��∅}{��t}$����綯�Ƶ�ƽ��ֵ��
��� �⣺��1�����ٶ�Ϊ����=2��n=20�У�
����������ֵΪ��Em=NBS��=100��0.1��0.1��20��=20��v
����Чֵ��E=$\frac{{E}_{m}}{\sqrt{2}}=\frac{20��}{\sqrt{2}}=10\sqrt{2}��V$��
����I=$\frac{E}{R+r}=\frac{10\sqrt{2}��}{10}$=$\sqrt{2}$��A
��ѹ����ʾ����U=$\frac{{E}_{��}}{R+r}$R=5$\sqrt{2}$��V
��2���綯��˲ʱֵ����ʽe=Emcos2��nt����t=$\frac{1}{60}$sʱ��e=10��=31.4V
��3������������ڣ�T=$\frac{2��}{��}$=0.1s��
ת��30�Ƚ�����ʱ��Ϊ��t=$\frac{1}{12}T=\frac{1}{120}s$��
��ƽ���綯��$\overline{E}=\frac{n��∅}{��t}=\frac{100��1��0.01��0.5}{\frac{1}{120}}=60V$
�𣺣�1����ѹ����ʾ��Ϊ5$\sqrt{2}$��V��������ʾ��Ϊ$\sqrt{2}$��A��
��2����ͼʾλ�ÿ�ʼ����$\frac{1}{60}$sʱ��Ӧ�綯�Ƶ�˲ʱֵΪ31.4V��
��3������ͼ��ʾλ�ÿ�ʼת��30��ǵĹ����е�ƽ����Ӧ�綯��ֵΪ60V��
���� �����ۺ��Խ�ǿ�������˷�ֵ����Чֵ�Ĺ�ϵ��˲ʱֵ����ʽ��ƽ��ֵ��Ӧ�ú��ܹ�ϵ��ע�������ʱҪ��ƽ��ֵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
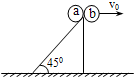 ��ͼ��ʾ��a��b��������Ϊm��a�����Ϊ450�Ĺ⻬�̶�б�涥�����ٶ��»���bͬʱ��б�涥�����ٶ�v0ˮƽ�׳����Զ����˶���������˵����ȷ���ǣ�������
��ͼ��ʾ��a��b��������Ϊm��a�����Ϊ450�Ĺ⻬�̶�б�涥�����ٶ��»���bͬʱ��б�涥�����ٶ�v0ˮƽ�׳����Զ����˶���������˵����ȷ���ǣ�������| A�� | ���ǰ��˲�����������ͬ | B�� | �����ٶ�ʼ����ͬ | ||
| C�� | a��b�����ȱ����˶� | D�� | a��bͬʱ��� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ʹ���������������Сһ�룬���벻�� | |
| B�� | ʹ����һ�������������С��ԭ����$\frac{1}{4}$�����벻�� | |
| C�� | ʹ�������ľ�����Ϊԭ����2������������ | |
| D�� | ʹ�������ľ������������Ϊԭ����$\frac{1}{4}$�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ�����������ˮƽ���30��ǣ���ǿ�ų��ĴŸ�ǿ��B=0.4T������ֱ���ƽ�����ϣ���������L=0.5m������Ϊ0.1N�������ڿ������Ħ���ػ����������ܵ��ܵ���Ϊ2���������㹻�����ʣ�
��ͼ��ʾ�����������ˮƽ���30��ǣ���ǿ�ų��ĴŸ�ǿ��B=0.4T������ֱ���ƽ�����ϣ���������L=0.5m������Ϊ0.1N�������ڿ������Ħ���ػ����������ܵ��ܵ���Ϊ2���������㹻�����ʣ��鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ˮƽ��⻬ʱ��F������������ƽ�����ʴ� | |
| B�� | ˮƽ�治�⻬��F������������ƽ�����ʽϴ� | |
| C�� | ˮƽ��⻬ʱ��F������������˲ʱ���ʽϴ� | |
| D�� | ˮƽ�治�⻬��F������������˲ʱ���ʽϴ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ���������ΪM=$\frac{4{��}^{2}{r}^{3}}{G{{T}_{2}}^{2}}$ | |
| B�� | ������ܶ�Ϊ��=$\frac{3��{r}^{3}}{G{T}^{3}{{T}_{1}}^{2}}$ | |
| C�� | ��������������ٶ�Ϊg=$\frac{4{��}^{2}R}{{{T}_{1}}^{2}}$ | |
| D�� | �����˶������ļ��ٶ�Ϊ$a=\frac{{4{��^2}r}}{T_1^2}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
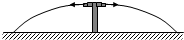 ��ͼ����ˮ����е������ظ�0.8m���ٶ�ˮ������ˮƽ��������뾶Ϊ4m�����ƿ���������ȡg=10m/s2����
��ͼ����ˮ����е������ظ�0.8m���ٶ�ˮ������ˮƽ��������뾶Ϊ4m�����ƿ���������ȡg=10m/s2�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
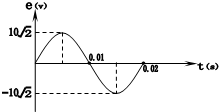 ������Ȧ����ǿ�ų�������ת�������ĸ�Ӧ�綯����ʱ��仯��ͼ����ͼ��ʾ��������ԭ������Ȧ����֮��Ϊn1��n2=1��10�������ѹ��ԭ��Ȧ���ˣ�������
������Ȧ����ǿ�ų�������ת�������ĸ�Ӧ�綯����ʱ��仯��ͼ����ͼ��ʾ��������ԭ������Ȧ����֮��Ϊn1��n2=1��10�������ѹ��ԭ��Ȧ���ˣ�������| A�� | ��ѹ������Ȧ���˵ĵ�ѹΪU2=100V | |
| B�� | ��Ӧ�綯�Ƶ�˲ʱֵ����ʽΪe=10 $\sqrt{2}$sin��t��V�� | |
| C�� | t=0.005��ʱ��������Ȧƽ��Ĵ�ͨ����� | |
| D�� | t=0.005��ʱ����Ȧƽ����ų�����ֱ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com