已知地球半径为R,一只静止在赤道上空的热气球(不计气球离地高度)绕地心运动的角速度为ω,在距地面h高处圆形轨道上有一颗人造地球卫星,设地球质量为M,热气球的质量为m,人造地球卫星的质量为m1,根据上述条件,有一位同学列出了以下两个方程:
对热气球有:GmM/R 2=mω2R 对人造卫星有:Gm1M/(R+h)2=m1ω2(R+h)
进而求出了人造地球卫星绕地球运行的角速度ω.你认为该同学的解法是否正确?若认为正确,请求出结果;若认为错误,请补充一个条件后,再求出ω.
【答案】
分析:那个气球的整个条件都是没用的,用来混淆视线的,这里卫星的角速度无法通过气球来求.只是这个题是找错题,他对气球的解答是错的,他错在对气球的受力分析上,气球受的万有引力不全是提供向心力,而是一部分与浮力平衡,而在求卫星角速度上,他不起什么作用.
要求出人造地球卫星绕地球运行的角速度ω,我们应补充一个条件后列出等式表示出GM.
解答:解:第一个等式(对热气球)解法不正确,因为热气球不同于人造卫星,热气球静止在空中是因为浮力与重力平衡.它受地球的引力并不等于它绕地心所需的向心力.
(1)若利用第一宇宙速度v
1,有

=

与第二个等式联立可得ω=v
1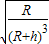
(2)若已知地球表面的重力加速度g,设地球质量为M,热气球质量为m,人造卫星质量为m
1 对热气球有:

=mg 对人造卫星有:

=m
1ω
2(R+h)
联立上两式解得:
ω=

.
(3)若利用同步卫星的离地高度H有:

=mω
2(R+H)
与第二个等式联到可得:ω=ω

答:该同学的解法是不正确.
若利用第一宇宙速度v
1,ω=v
1
.
若已知地球表面的重力加速度g,ω=

若利用同步卫星的离地高度H,ω=ω

.
补充其它条件解法正确给全分.
点评:本题考查了万有引力在天体中的应用,解题的关键在于找出向心力的来源,并能列出等式解题.
要注意热气球受地球的引力并不等于它绕地心所需的向心力.

 =
=
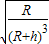
 =mg 对人造卫星有:
=mg 对人造卫星有: =m1ω2(R+h)
=m1ω2(R+h)  .
.  =mω2(R+H)
=mω2(R+H)
 .
.
 .
.
