
| A. | 月球绕地球的运行周期T和月球中心到地球中心间距离R | |
| B. | 人造地球卫星在地面附近运行的速度v和运行周期T | |
| C. | 地球绕太阳运行的周期T和地球中心到太阳中心的距离R | |
| D. | 地球半径R和地球表面重力加速度g |
分析 地球、月球、人造卫星等做匀速圆周运动,它们受到的万有引力充当向心力,用它们的运动周期表示向心力,由万有引力定律结合牛顿第二定律列式求中心天体的质量.在地球表面的物体受到的重力等于万有引力,因此已知地球半径R和地球表面重力加速度g,也可以计算地球质量
解答 解:A、月球绕地球做匀速圆周运动,它受到地球的万有引力充当向心力,用它运动周期表示向心力,由万有引力定律结合牛顿第二定律得:G$\frac{Mm}{{R}^{2}}$=mR$\frac{4{π}^{2}}{{T}^{2}}$,解得地球的质量M=$\frac{4{π}^{2}{R}^{3}}{G{T}^{2}}$,因此,可求出地球的质量.
B、人造卫星绕地球做匀速圆周运动,它受到地球的万有引力充当向心力,用它运动周期表示向心力,
由万有引力定律结合牛顿第二定律得:G$\frac{Mm}{{R}^{2}}$=m$\frac{4{π}^{2}}{{T}^{2}}$R,又因T=$\frac{2πR}{V}$,所以地球的质量M=$\frac{T{V}^{3}}{2πG}$,因此,可求出地球的质量.
C、地球绕太阳做匀速圆周运动,受到太阳的万有引力充当向心力,用它运动周期表示向心力,
由万有引力定律结合牛顿第二定律得:G$\frac{Mm}{{R}^{2}}$=m$\frac{4{π}^{2}}{{T}^{2}}$R,所以太阳的质量M=$\frac{4{π}^{2}{R}^{3}}{G{T}^{2}}$,因此,不能求出地球的质量.
D、在地球表面的物体受到的重力等于万有引力mg=G$\frac{Mm}{{R}^{2}}$,所以地球质量M=$\frac{g{R}^{2}}{G}$.
本题选不能的,故选:C
点评 解答万有引力定律在天体运动中的应用时要明确天体做匀速圆周运动,其受到的万有引力提供向心力,会用线速度、角速度、周期表示向心力,同时注意公式间的化简


科目:高中物理 来源: 题型:多选题
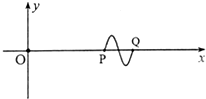 O、P、Q是x轴上的三点,OP=6m,OQ=8m.t=0时刻位于O点的振源完成一次全振动,发出一个振幅为0.4m的完整波,t=0.4s时刻,x轴上的波形如图所示.t=1.0s时刻,位于O点的振源又完成一次全振动,发出另一个与第一列波起振方向相同、振幅相同、频率不同的完整波,t=1.9s时刻,P点刚好在x轴上方最高点,则以下说法正确的是( )
O、P、Q是x轴上的三点,OP=6m,OQ=8m.t=0时刻位于O点的振源完成一次全振动,发出一个振幅为0.4m的完整波,t=0.4s时刻,x轴上的波形如图所示.t=1.0s时刻,位于O点的振源又完成一次全振动,发出另一个与第一列波起振方向相同、振幅相同、频率不同的完整波,t=1.9s时刻,P点刚好在x轴上方最高点,则以下说法正确的是( )| A. | 第一列波的起振方向向上 | |
| B. | 第一列波的传播周期为0.1s | |
| C. | 两列波的传播速度相同 | |
| D. | 第二列波的传播周期为0.8s | |
| E. | 质点P在这1.9s内通过的路程为2.0m |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题

| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图,电阻为R的长直螺线管,其两端通过电阻可忽略的导线相连接.一个质量为m的小条形磁铁从静止开始落入其中,下落一段距离后以速度v做匀速运动.假设小磁铁在下落过程中始终沿螺线管的轴线运动且无翻转.则 ( )
如图,电阻为R的长直螺线管,其两端通过电阻可忽略的导线相连接.一个质量为m的小条形磁铁从静止开始落入其中,下落一段距离后以速度v做匀速运动.假设小磁铁在下落过程中始终沿螺线管的轴线运动且无翻转.则 ( )| A. | 小磁铁的磁性越强,最后匀速运动的速度就越大 | |
| B. | 小磁铁的磁性越强,它经过同一位置时的加速度越大 | |
| C. | 小磁铁做匀速运动时在回路中产生的感应电流为零 | |
| D. | 小磁铁做匀速运动时在回路中产生的感应电动势为$\sqrt{mgRv}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
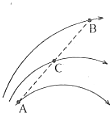 如图所示是某电场中的三条电场线,C点时A、B连线的中点.已知A点的电势是φA=30V,B点的电势φB=-20V,则下列说法正确的是( )
如图所示是某电场中的三条电场线,C点时A、B连线的中点.已知A点的电势是φA=30V,B点的电势φB=-20V,则下列说法正确的是( )| A. | C点的电势φC=5V | |
| B. | C点的电势φC>5V | |
| C. | C点的电势φC<5V | |
| D. | 负电荷在A点的电势能大于在B点的电势能 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 甲、乙两辆汽车在同一平直公路上行驶,其速度时间图象如图所示,已知两辆汽车在25s末到达同一位置,则甲、乙两辆汽车( )
甲、乙两辆汽车在同一平直公路上行驶,其速度时间图象如图所示,已知两辆汽车在25s末到达同一位置,则甲、乙两辆汽车( )| A. | 运动的加速度之比为5:1 | |
| B. | 相遇前的平均速度相等 | |
| C. | 到达同一位置前相距最远距离为180m | |
| D. | 到达同一位置前相距最远距离为400m |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
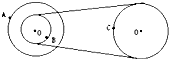 如图所示的皮带传动装置中,轮A和B同轴,A、B、C分别是三个轮边缘的质点,且RA=RC=2RB,则下列说法中正确的是( )
如图所示的皮带传动装置中,轮A和B同轴,A、B、C分别是三个轮边缘的质点,且RA=RC=2RB,则下列说法中正确的是( )| A. | 三质点的线速度之比vA:vB:vC=2:1:1 | |
| B. | 三质点的角速度之比ωA:ωB:ωC=2:1:1 | |
| C. | 三质点的周期之比TA:TB:TC=2:2:1 | |
| D. | 三质点的频率之比fA:fB:fC=1:1:1 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,在x>0、y>0的空间有方向垂直于xOy平面向里的匀强磁场.现有两个质量及电荷量均相同的带电粒子,由x轴上的P点以不同的初速度平行于y轴射入此磁场,然后分别从y轴上的M、N两点射出磁场,不计粒子重力及它们间的相互作用.比较两粒子的运动,下列说法正确的是( )
如图所示,在x>0、y>0的空间有方向垂直于xOy平面向里的匀强磁场.现有两个质量及电荷量均相同的带电粒子,由x轴上的P点以不同的初速度平行于y轴射入此磁场,然后分别从y轴上的M、N两点射出磁场,不计粒子重力及它们间的相互作用.比较两粒子的运动,下列说法正确的是( )| A. | 从N点射出的粒子初速度较大 | |
| B. | 从N点射出的粒子在磁场中的加速度较大 | |
| C. | 从M点射出的粒子在磁场中的角速度较大 | |
| D. | 从M点射出的粒子在磁场中的时间较短 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com