
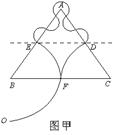
(16分)为了使粒子经过一系列的运动后,又以原来的速率沿相反方向回到原位,可设计如下的一个电磁场区域(如图所示):水平线QC以下是水平向左的匀强电场,区域Ⅰ(梯形PQCD)内有垂直纸面向里的匀强磁场,磁感应强度为B;区域Ⅱ(三角形APD)内的磁场方向与Ⅰ内相同,但是大小可以不同,区域Ⅲ(虚线PD之上、三角形APD以外)的磁场与Ⅱ内大小相等、方向相反.已知等边三角形AQC的边长为2l,P、D分别为AQ、AC的中点.带正电的粒子从Q点正下方、距离Q点为l的O点以某一速度射出,在电场力作用下从QC边中点N以速度v0垂直QC射入区域Ⅰ,再从P点垂直AQ射入区域Ⅲ,又经历一系列运动后返回O点.(粒子重力忽略不计)求: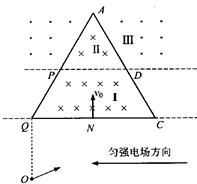
(1)该粒子的比荷.
(2)粒子从O点出发再回到O点的整个运动过程所需时间.
(1)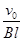 (2)
(2)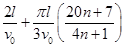 或
或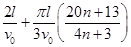
解析试题分析:本题属于带电粒子在组合场中运动问题,磁场中圆周运动要画轨迹分析运动过程,探索规律,寻找半径与三角形边的关系是关键.
(1)从N到P,做匀速圆周运动,根据牛顿第二定律和洛仑兹力表达式有: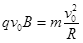
根据题意有R=l 解得: 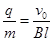
(2)粒子从O到N与从N到O是逆过程,N到O做类平抛运动,在区域Ⅰ、区域Ⅱ和Ⅲ中都做匀速圆周运动.带电粒子在电磁场中运动的总时间包括三段:电场中往返的时间t0、区域Ⅰ中的时间t1、区域Ⅱ和Ⅲ中的时间t2+t3
根据平抛运动规律有 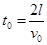
粒子在区域Ⅰ中运动时,由线速度和角速度关系得: 即
即
①若粒子在区域Ⅱ和Ⅲ内的运动如图甲所示,则总路程为 个圆周,根据几何关系有
个圆周,根据几何关系有
AE=(4nr + r)=l 解得: r=l/(4n + 1) 其中n=0,1,2……
区域Ⅱ和Ⅲ内总路程为

总时间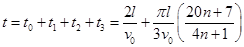

②若粒子在区域Ⅱ和Ⅲ内运动如图乙所示,则总路程为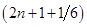 个圆周,根据几何关系有:
个圆周,根据几何关系有:
AP=(4nr +3r)=l 解得: r= l/(4n + 3) 其中n=0,1,2……
区域Ⅱ和Ⅲ内总路程为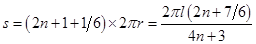
总时间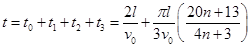
考点:本题考查了带电粒子在电场和磁场中的运动、匀速圆周运动规律、牛顿第二定律、向心力、运动的合成与分解,同时考查考生的分析综合能力和运用数学知识解决物理问题的能力.


科目:高中物理 来源: 题型:计算题
(10分)如图所示,两根平行且光滑的金属轨道固定在斜面上,斜面与水平面之间的夹角 ,轨道上端接一只阻值为R=0.4
,轨道上端接一只阻值为R=0.4 的电阻器,在导轨间存在垂直于导轨平面的匀强磁场,磁场的磁感应强度B=0.5 T,两轨道之间的距离为L=40cm,且轨道足够长,电阻不计。现将一质量为m="3" g,有效电阻为r=1.0
的电阻器,在导轨间存在垂直于导轨平面的匀强磁场,磁场的磁感应强度B=0.5 T,两轨道之间的距离为L=40cm,且轨道足够长,电阻不计。现将一质量为m="3" g,有效电阻为r=1.0 的金属杆ab放在轨道上,且与两轨道垂直,然后由静止释放,求:
的金属杆ab放在轨道上,且与两轨道垂直,然后由静止释放,求:
(1)金属杆ab下滑过程中可达到的最大速率;
(2)金属杆ab达到最大速率以后,电阻器R每秒内产生的电热。
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
(14分)如图所示,竖直平面内有两光滑金属圆轨道,平行正对放置,直径均为d,电阻不计。某金属棒长L、质量m、电阻r,放在圆轨道最低点MM' 处,与两导轨刚好接触。两圆轨道通过导线与电阻R相连。空间有竖直向上的匀强磁场,磁感应强度为B。现使金属棒获得垂直纸面向里的初速度vo,当其沿圆轨道滑到最高点NN' 处时,对轨道恰无压力(滑动过程中金属棒与圆轨道始终接触良好)。重力加速度为g,求: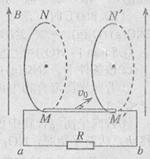
(1)金属棒刚获得垂直纸面向里的初速度时,判断电阻R中电流的方向;
(2)金属棒到达最高点NN' 处时,电路中的电功率;
(3)金属棒从MM' 处滑到NN' 处的过程中,电阻R上产生的焦耳热。
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
如图所示,竖直面内有一绝缘轨道,AB部分是光滑的四分之一圆弧,圆弧半径R=0.5m,B处切线水平,BC部分为水平粗糙直轨道。有一个带负电的小滑块(可视为质点)从A点由静止开始下滑,运动到直轨道上的P处刚好停住。小滑块的质量m=1kg,带电量为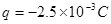 保持不变,滑块小轨道BC部分间的动摩擦因数为μ=0.2,整个空间存在水平向右的匀强电场,电场强度大小为E=4.0×102N/C.(g=10m/s2)
保持不变,滑块小轨道BC部分间的动摩擦因数为μ=0.2,整个空间存在水平向右的匀强电场,电场强度大小为E=4.0×102N/C.(g=10m/s2) 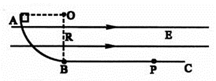
(1)求滑块到达B点瞬间的速度大小
(2)求滑块到达B点瞬间对轨道的压力大小。
(3)求BP间的距离,
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
(18分)如图所示,相距为R的两块平行金属板M、 N正对着放置,S1、S2分别为M、N板上的小孔,S1、S2、O三点共线,它们的连线垂直M、N,且S2O=R.以O为圆心、R为半径的圆形区域内存在磁感应强度为B、方向垂直纸面向外的匀强磁场.D为收集板,板上各点到O点的距离以及板两端点的距离都为2R,板两端点的连线垂直M、N板.质量为m、带电量为+q的粒子经S1进入M、N间的电场后,通过S2进入磁场.粒子在S1处的速度以及粒子所受的重力均不计.
(1)M、N间的电压为U时,求粒子进入磁场时速度的大小v;
(2)若粒子恰好打在收集板D的中点上,求M、N间的电压值U0;
(3)当M、N间的电压不同时,粒子从S1到打在D上经历的时间t会不同,求
t的最小值.
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
(18分)如图为某同学设计的速度选择装置,两根足够长的光滑导轨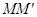 /和
/和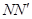 间距为L与水平方向成
间距为L与水平方向成 角,上端接滑动变阻器R,匀强磁场
角,上端接滑动变阻器R,匀强磁场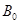 垂直导轨向上,金属棒ab质量为
垂直导轨向上,金属棒ab质量为 垂直横跨在导轨上。滑动变阻器R两端连接水平放置的平行金属板,极板间距为d,板长为2d,匀强磁场B垂直纸面向内。粒子源能发射沿水平方向不同速率的带电粒子,粒子的质量为
垂直横跨在导轨上。滑动变阻器R两端连接水平放置的平行金属板,极板间距为d,板长为2d,匀强磁场B垂直纸面向内。粒子源能发射沿水平方向不同速率的带电粒子,粒子的质量为 ,电荷量为q,ab棒的电阻为r,滑动变阻器的最大阻值为2r,其余部分电阻不计,不计粒子重力。
,电荷量为q,ab棒的电阻为r,滑动变阻器的最大阻值为2r,其余部分电阻不计,不计粒子重力。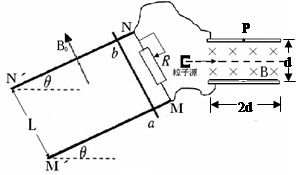
(1)ab棒静止未释放时,某种粒子恰好打在上极板中点P上,该粒子带何种电荷?该粒子的速度多大?
(2)调节变阻器使R=0.5r,然后释放ab棒,求ab棒的最大速度?
(3)当ab棒释放后达到最大速度时,若变阻器在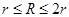 范围调节,总有粒子能匀速穿过平行金属板,求这些粒子的速度范围?
范围调节,总有粒子能匀速穿过平行金属板,求这些粒子的速度范围?
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
(18分)如图,xoy平面内存在着沿y轴正方向的匀强电场,一个质量为m、带电荷量为+q的粒子从坐标原点O以速度v0沿x轴正方向开始运动。当它经过图中虚线上的M(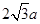 ,a)点时,撤去电场,粒子继续运动一段时间后进入一个矩形匀强磁场区域(图中未画出),又从虚线上的某一位置N处沿y轴负方向运动并再次经过M点。已知磁场方向垂直xoy平面(纸面)向里,磁感应强度大小为B,不计粒子的重力。试求:
,a)点时,撤去电场,粒子继续运动一段时间后进入一个矩形匀强磁场区域(图中未画出),又从虚线上的某一位置N处沿y轴负方向运动并再次经过M点。已知磁场方向垂直xoy平面(纸面)向里,磁感应强度大小为B,不计粒子的重力。试求: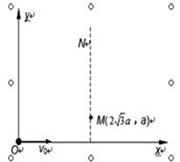
⑴电场强度的大小;
⑵N点的坐标;
⑶矩形磁场的最小面积。
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
(18分)中心均开有小孔的金属板C、D与半径为d的圆形单匝金属线圈连接,圆形框内有垂直纸面的匀强磁场,大小随时间变化的关系为B=kt(k未知且k>0),E、F为磁场边界,且与C、D板平行。D板右方分布磁场大小均为B0,方向如图所示的匀强磁场。区域Ⅰ的磁场宽度为d,区域Ⅱ的磁场宽度足够。在C板小孔附近有质量为m、电量为q的负离子由静止开始加速后,经D板小孔垂直进入磁场区域Ⅰ,不计离子重力。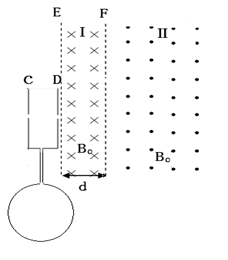
(1)判断圆形线框内的磁场方向;
(2)若离子从C板出发,运动一段时间后又恰能回到C板出发点,求离子在磁场中运动的总时间;
(3)若改变圆形框内的磁感强度变化率k,离子可从距D板小孔为2d的点穿过E边界离开磁场,求圆形框内磁感强度的变化率k是多少?
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
(18分)如图所示,在水平直角坐标系xOy中的第一象限内存在磁感应强度大小为B、方向垂直于坐标平面向内的有界圆形匀强磁场区域(图中未画出);在第二象限内存在沿x轴负方向的匀强电场。一粒子源固定在x轴上的A点,A点坐标为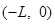 . 粒子源沿y轴正方向释放出速度大小为v的电子,电子恰好能通过y轴上的C点,C点坐标为(0,2L),电子经过磁场偏转后方向恰好垂直ON,ON是与x轴正方向成
. 粒子源沿y轴正方向释放出速度大小为v的电子,电子恰好能通过y轴上的C点,C点坐标为(0,2L),电子经过磁场偏转后方向恰好垂直ON,ON是与x轴正方向成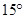 角的射线.(电子的质量为m,电荷量为e,不考虑粒子的重力和粒子之间的相互作用.)求:
角的射线.(电子的质量为m,电荷量为e,不考虑粒子的重力和粒子之间的相互作用.)求: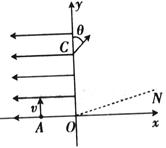
(1)第二象限内电场强度E的大小.
(2)电子离开电场时的速度方向与y轴正方向的夹角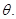
(3)圆形磁场的最小半径Rmin.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com