
 ��ͼ��ʾ��ƽ�е�������ͬһˮƽ���ϣ�������ΪL����˽ӵ���R�������ڴ�����ֱ���ϵĴŸ�Ӧǿ��ΪB���н���ǿ�ų�����߽�MNPQΪһ���߳�Ϊa�������Σ������εı��뵼���45�㣮��M��Ϊԭ�㣬��MP��x�ᣮһ������Ϊm�Ĺ⻬�����ˣ�������Բ��ƣ���ֱ���ڵ����ϣ�����x������F�������£���M�㴦�Ժ㶨�ٶ�v��x���������˶����ʣ�
��ͼ��ʾ��ƽ�е�������ͬһˮƽ���ϣ�������ΪL����˽ӵ���R�������ڴ�����ֱ���ϵĴŸ�Ӧǿ��ΪB���н���ǿ�ų�����߽�MNPQΪһ���߳�Ϊa�������Σ������εı��뵼���45�㣮��M��Ϊԭ�㣬��MP��x�ᣮһ������Ϊm�Ĺ⻬�����ˣ�������Բ��ƣ���ֱ���ڵ����ϣ�����x������F�������£���M�㴦�Ժ㶨�ٶ�v��x���������˶����ʣ����� ��1������Em=BLvȷ������и���������Ӧ�綯�ƣ�����ŷķ����������ǿ�ȣ������ֶ����жϵ�������
��2����������ƶ�λ�Ƽ�Ϊx�������Ч�и����x�Ĺ�ϵ��������ǿ�ȴ�С���ٸ��ݰ������ļ��㹫ʽ��ⰲ������x�ķ����ɴ˵õ�������x�Ĺ�ϵ��
��� �⣺��1���������֪����������QN����x=$\frac{\sqrt{2}}{2}$aʱ��
��ʱ��Ӧ�綯��EmΪ��Em=BLQNv=$\sqrt{2}$Bav��
��Ӧ����ImΪ��Im=$\frac{{E}_{m}}{R}$=$\frac{\sqrt{2}Bav}{R}$��
��Ӧ����������ͼ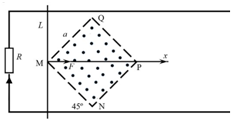
��2���������֪�������ƶ�λ�Ƽ�Ϊx��
������FAx=BIxLx
${I}_{x}=\frac{{E}_{x}}{R}$��Ex=BLxv��
����FAx=$\frac{{B}^{2}{L}_{x}^{2}v}{R}$��
��0��x��$\frac{\sqrt{2}}{2}$aʱ��Lx=2x
����F���ڰ�����FA����F=FA=$\frac{{B}^{2}{L}_{x}^{2}v}{R}$=$\frac{4{{B}^{2}x}^{2}v}{R}$��
��$\frac{\sqrt{2}}{2}$a��x��$\sqrt{2}$aʱ��Lx=$2��\sqrt{2}a-x��$��
����F���ڰ�����FA����F=FA=$\frac{4{B}^{2}��\sqrt{2}a-x��^{2}v}{R}$
��x��$\sqrt{2}$aʱ��Lx=0
����F=FA=0��
�𣺣�1����������$\frac{\sqrt{2}}{2}$a�������ĸ�Ӧ�����������Ӧ����Ϊ$\frac{\sqrt{2}Bav}{R}$���������������ͼ��
��2��0��x��$\frac{\sqrt{2}}{2}$aʱ��F=$\frac{{B}^{2}{L}_{x}^{2}v}{R}$=$\frac{4{{B}^{2}x}^{2}v}{R}$��
��$\frac{\sqrt{2}}{2}$a��x��$\sqrt{2}$aʱ��F=$\frac{4{B}^{2}��\sqrt{2}a-x��^{2}v}{R}$��
��x��$\sqrt{2}$aʱ��F=0��
���� ������Ҫ�ǿ����˷����ڵ�Ÿ�Ӧ���ɺͰ������ļ��㣻���ڵ����и�Ÿ�Ӧ�߲����ĸ�Ӧ�綯�ƿ��Ը���E=BLv�����㣬ע��L�Ǵ�ֱ�ڴų��������Ч�и�ȣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ʵ����

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ��˹�ط����˵����Ĵ�ЧӦ���������˵�Ÿ�Ӧ���� | |
| B�� | ��η����˵����Ĵ�ЧӦ����ʾ�˴�����͵�����֮�����ϵ | |
| C�� | �ڷ����ڡ�Ŧ����Τ�����˹����Ļ����ϣ�������ʶ������·�и�Ӧ�綯�ƵĴ�С����������һ��·�Ĵ�ͨ���ı仯�ʳ����ȣ����˳�֮Ϊ�����ڵ�Ÿ�Ӧ���� | |
| D�� | �������ڷ���������ʵ����ʵ���������Ӧ����Ӧ���������ķ�����Ӧ�����Ĵų���Ҫ�谭�����Ӧ�����Ĵ�ͨ���ı仯 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �شų�����ǿ�ų� | |
| B�� | �شų����ϼ��ڵ�����ϼ����� | |
| C�� | �شų��ı����ڵ�����ϼ����� | |
| D�� | �ڵ����ı��������شų�����ֱ���ϵ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ��a=��2r��֪����r | B�� | ��a=$\frac{{v}^{2}}{r}$��֪a��$\frac{1}{r}$ | ||
| C�� | ��a=G$\frac{M}{{r}^{2}}$��֪a��$\frac{1}{{r}^{2}}$ | D�� | ��a=��v��֪a��r�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �Ⲩ�Ǹ��ʲ������ʲ����Ǹ��ʲ� | |
| B�� | ʵ�����Ӳ����в����� | |
| C�� | ʵ������Ҳ���в����ԣ�ֻ�Dz����� | |
| D�� | ��IJ������ǹ���֮������������ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
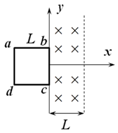 �ڹ⻬ˮƽ���ϣ���һ��ֱ���µ���ǿ�ų��ֲ��ڿ�ΪL�������ڣ��Ÿ�Ӧǿ��ΪB�������αպ���Ȧ�ı߳�ΪL����x���������˶���δ����ų�ʱ���ٶ�V0�����˶������ܴ�ֱ�ų��߽紩���ų�����ô��������
�ڹ⻬ˮƽ���ϣ���һ��ֱ���µ���ǿ�ų��ֲ��ڿ�ΪL�������ڣ��Ÿ�Ӧǿ��ΪB�������αպ���Ȧ�ı߳�ΪL����x���������˶���δ����ų�ʱ���ٶ�V0�����˶������ܴ�ֱ�ų��߽紩���ų�����ô��������| A�� | bc�߸ս���ų�ʱbc���˵ĵ�ѹΪ$\frac{BL{v}_{0}}{4}$ | |
| B�� | ��Ȧ����ų������еĵ�������Ϊ˳ʱ�뷽�� | |
| C�� | ��Ȧ����ų����ȼ���ֱ���˶� | |
| D�� | ��Ȧ����ų����̲����Ľ����ȴ����뿪�ų����̲����Ľ����� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
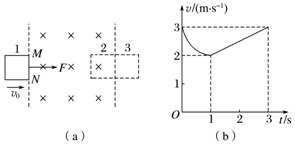 ��ͼ��a����ʾ���ڹ⻬ˮƽ���Ϸ���һ����Ϊ1kg�ĵ��Ѿ���������ͭ�߿��߿�߳�Ϊ0.1m������������������ֱ���µ���ǿ�ų����Ÿ�Ӧǿ��Ϊ$\frac{10}{3}$T�����ú���F���߿��߿�1λ��ʱ�����ٶ�v0=3m/s������ǿ�ų�����ʼ��ʱ����t=3sʱ���߿�2λ�ÿ�ʼ�뿪��ǿ�ų����˹�����v-tͼ����ͼ��b����ʾ����ô��������
��ͼ��a����ʾ���ڹ⻬ˮƽ���Ϸ���һ����Ϊ1kg�ĵ��Ѿ���������ͭ�߿��߿�߳�Ϊ0.1m������������������ֱ���µ���ǿ�ų����Ÿ�Ӧǿ��Ϊ$\frac{10}{3}$T�����ú���F���߿��߿�1λ��ʱ�����ٶ�v0=3m/s������ǿ�ų�����ʼ��ʱ����t=3sʱ���߿�2λ�ÿ�ʼ�뿪��ǿ�ų����˹�����v-tͼ����ͼ��b����ʾ����ô��������| A�� | t=0ʱ���߿��Ҳ������MN��ĵ�ѹΪ0.75 V | |
| B�� | ����F�Ĵ�СΪ0.5 N | |
| C�� | �߿���ȫ�뿪�ų���˲����ٶȴ�СΪ3 m/s | |
| D�� | �߿���ȫ�뿪�ų���˲����ٶȴ�СΪ1 m/s |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
 �ҹ�����2022��ٰ춬�»ᣬ��̨��ѩ��������߹����Ե���Ŀ֮һ����ͼ��ʾ������m=60kg���˶�Ա�ӳ�ֱ������AB��A���ɾ�ֹ��ʼ������������������Լ��ٶ�a=3.6m/s2�ȼ��ٻ��£�����B��ʱ�ٶ�vB=24m/s��A��B����ֱ�߶Ȳ�H=48m��Ϊ�˸ı��˶�Ա���˶�������������������̨D��֮����һ����������BCD�νӣ�B��C��ĸ߶Ȳ�h=5m��C��D��ĸ߶Ȳ�h��=4m������BCD�ϵ�Ħ����gȡ10m/s2����
�ҹ�����2022��ٰ춬�»ᣬ��̨��ѩ��������߹����Ե���Ŀ֮һ����ͼ��ʾ������m=60kg���˶�Ա�ӳ�ֱ������AB��A���ɾ�ֹ��ʼ������������������Լ��ٶ�a=3.6m/s2�ȼ��ٻ��£�����B��ʱ�ٶ�vB=24m/s��A��B����ֱ�߶Ȳ�H=48m��Ϊ�˸ı��˶�Ա���˶�������������������̨D��֮����һ����������BCD�νӣ�B��C��ĸ߶Ȳ�h=5m��C��D��ĸ߶Ȳ�h��=4m������BCD�ϵ�Ħ����gȡ10m/s2�����鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com